《2025年全程助学与学习评估八年级数学上册浙教版》

1. 将点 $ A(-3,-2) $ 向左平移 $ 5 $ 个单位,再向下平移 $ 4 $ 个单位得到点 $ B $,则点 $ B $ 的坐标为(B)
A.$ (-8,2) $
B.$ (-8,-6) $
C.$ (2,-2) $
D.$ (2,2) $

答案： B

2. 将三角形各边上的所有点的横坐标都减去 $ 2 $,纵坐标不变,则所得三角形与原三角形的关系是(A)
A.将原图向左平移 $ 2 $ 个单位
B.关于原点对称
C.将原图向右平移 $ 2 $ 个单位
D.关于 $ y $ 轴对称

答案： A

3. (1) 把点 $ P(-2,7) $ 向左平移 $ 2 $ 个单位,得到点$(-4,7)$.
(2) 把点 $ P(-2,7) $ 向下平移 $ 7 $ 个单位,得到点$(-2,0)$.
(3) 把以 $ (-2,7) $,$ (-2,-2) $ 为端点的线段向右平移 $ 7 $ 个单位,所得图象上任意一点的坐标可表示为$(5,y)(-2 \leq y \leq 7)$（或写成$(5,t), -2 \leq t \leq 7$ 等类似形式）.

答案：
(1) $(-4,7)$；
(2) $(-2,0)$；
(3) $(5,y)(-2 \leq y \leq 7)$（或写成$(5,t), -2 \leq t \leq 7$ 等类似形式）。

4. 如图,在直角坐标系中,图案甲经过平移得到图案乙,图案乙中左、右两只眼睛的坐标分别是 $ (-4,2) $,$ (-2,2) $,图案甲中左眼的坐标是 $ (3,4) $,则图案甲中右眼的坐标是______.

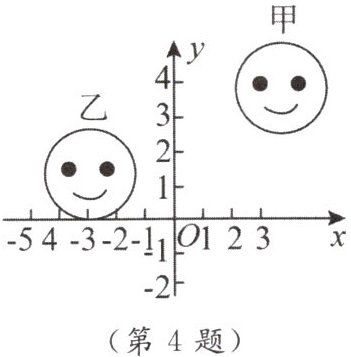
(5,4)

答案： (5,4)

5. 已知点 $ A(a,5) $ 向左平移 $ 2 $ 个单位后变为 $ (2,b) $,求 $ (a - b)^{2023} $ 的值.

答案： 由题意，点$A(a,5)$向左平移$2$个单位后，横坐标减少$2$，纵坐标不变，得到新坐标为$(a-2,5)$。
根据题目，这个新坐标等于$(2,b)$，所以：
$a - 2 = 2$，
$5 = b$，
从上面的方程组，解得：
$a = 4$，
$b = 5$，
代入$a$和$b$的值到$(a - b)^{2023}$中，得：
$(4 - 5)^{2023} = (-1)^{2023} = -1$，
所以，$(a - b)^{2023} = -1$。