7. 某同学在研究传统文化“抖空竹”时有一个发现,他把“抖空竹”抽象成数学问题,如图,已知$AB // CD$,$\angle BAE = 87^{\circ}$,$\angle DCE = 121^{\circ}$,则$\angle E$的度数是(
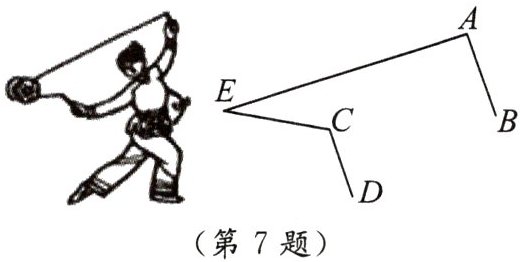
A.$28^{\circ}$
B.$34^{\circ}$
C.$46^{\circ}$
D.$56^{\circ}$
]
B
)
A.$28^{\circ}$
B.$34^{\circ}$
C.$46^{\circ}$
D.$56^{\circ}$
]
答案:
B
8. 已知$l_{1} // l_{2}$,直线$l与l_{1}$,$l_{2}相交于C$,$D$两点,将一把含$30^{\circ}$角的三角尺按如图所示的位置摆放.若$\angle 1 = 130^{\circ}$,则$\angle 2 = $
]
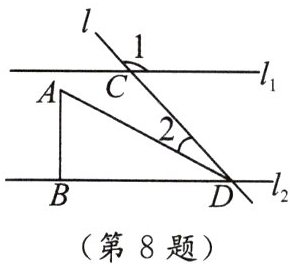
20
.]

答案:
20
9. 如图,已知直线$AB // CD$,直线$EF分别交AB$,$CD于M$,$N$,$MP平分\angle EMB$,$NQ平分\angle MND$.求证:$MP // NQ$.
]
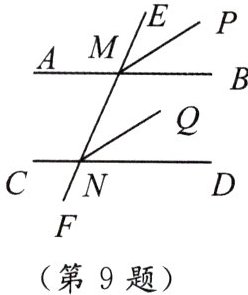
]

答案:
证明:
∵AB//CD(已知),
∴∠EMB=∠MND(两直线平行,同位角相等)。
∵MP平分∠EMB(已知),
∴∠EMP=1/2∠EMB(角平分线定义)。
∵NQ平分∠MND(已知),
∴∠MNQ=1/2∠MND(角平分线定义)。
∴∠EMP=∠MNQ(等量代换)。
∴MP//NQ(同位角相等,两直线平行)。
∵AB//CD(已知),
∴∠EMB=∠MND(两直线平行,同位角相等)。
∵MP平分∠EMB(已知),
∴∠EMP=1/2∠EMB(角平分线定义)。
∵NQ平分∠MND(已知),
∴∠MNQ=1/2∠MND(角平分线定义)。
∴∠EMP=∠MNQ(等量代换)。
∴MP//NQ(同位角相等,两直线平行)。
10. 已知$AB // CD$,$\angle ABE与\angle CDE的平分线交于点F$.
(1)如图$1$,若$\angle E = 80^{\circ}$,求$\angle BFD$的度数.
(2)如图$2$,$\angle ABM = \frac{1}{3}\angle ABF$,$\angle CDM = \frac{1}{3}\angle CDF$,写出$\angle M与\angle E$之间的数量关系,并证明你的结论.
★(3)若$\angle ABM = \frac{1}{n}\angle ABF$,$\angle CDM = \frac{1}{n}\angle CDF$,设$\angle E = m^{\circ}$,则$\angle M = $
]
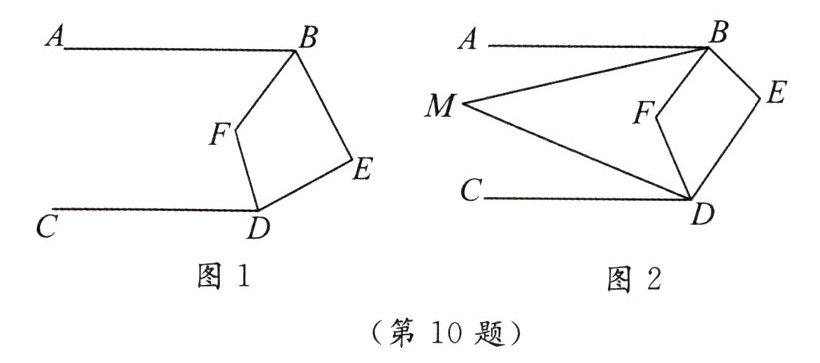
(1)如图$1$,若$\angle E = 80^{\circ}$,求$\angle BFD$的度数.
(2)如图$2$,$\angle ABM = \frac{1}{3}\angle ABF$,$\angle CDM = \frac{1}{3}\angle CDF$,写出$\angle M与\angle E$之间的数量关系,并证明你的结论.
★(3)若$\angle ABM = \frac{1}{n}\angle ABF$,$\angle CDM = \frac{1}{n}\angle CDF$,设$\angle E = m^{\circ}$,则$\angle M = $
$\frac{360 - m}{2n}$
(用含$n$,$m$的代数式表示,不用证明).]

答案:
(1) 过点F作FH//AB,
∵AB//CD,
∴FH//CD。
∵BF平分∠ABE,DF平分∠CDE,设∠ABF=∠FBE=x,∠CDF=∠FDE=y。
∵FH//AB,
∴∠BFH=∠ABF=x;
∵FH//CD,
∴∠DFH=∠CDF=y。
∴∠BFD=∠BFH+∠DFH=x+y。
过点E作EG//AB,
∵AB//CD,
∴EG//CD。
则∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°。
∵∠BED=80°,
∴2x+2y+80°=360°,
∴x+y=140°。
∴∠BFD=140°。
(2) ∠E=360°-6∠M。
证明:设∠ABF=x,∠CDF=y,由
(1)知x+y=180°-∠E/2。
∵∠ABM=1/3∠ABF=x/3,∠CDM=1/3∠CDF=y/3。
过点M作MN//AB,
∵AB//CD,
∴MN//CD。
则∠BMN=∠ABM=x/3,∠DMN=∠CDM=y/3,
∴∠M=∠BMN+∠DMN=(x+y)/3。
∴x+y=3∠M,
∴3∠M=180°-∠E/2,
∴∠E=360°-6∠M。
(3) (360 - m)/(2n)°
(1) 过点F作FH//AB,
∵AB//CD,
∴FH//CD。
∵BF平分∠ABE,DF平分∠CDE,设∠ABF=∠FBE=x,∠CDF=∠FDE=y。
∵FH//AB,
∴∠BFH=∠ABF=x;
∵FH//CD,
∴∠DFH=∠CDF=y。
∴∠BFD=∠BFH+∠DFH=x+y。
过点E作EG//AB,
∵AB//CD,
∴EG//CD。
则∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°。
∵∠BED=80°,
∴2x+2y+80°=360°,
∴x+y=140°。
∴∠BFD=140°。
(2) ∠E=360°-6∠M。
证明:设∠ABF=x,∠CDF=y,由
(1)知x+y=180°-∠E/2。
∵∠ABM=1/3∠ABF=x/3,∠CDM=1/3∠CDF=y/3。
过点M作MN//AB,
∵AB//CD,
∴MN//CD。
则∠BMN=∠ABM=x/3,∠DMN=∠CDM=y/3,
∴∠M=∠BMN+∠DMN=(x+y)/3。
∴x+y=3∠M,
∴3∠M=180°-∠E/2,
∴∠E=360°-6∠M。
(3) (360 - m)/(2n)°
查看更多完整答案,请扫码查看


