《2025年全程助学与学习评估八年级数学上册浙教版》

1. 如果两条平行线被第三条直线所截,那么一组内错角的平分线(B)
A.互相垂直
B.互相平行
C.互相重合
D.以上均不正确

答案： B

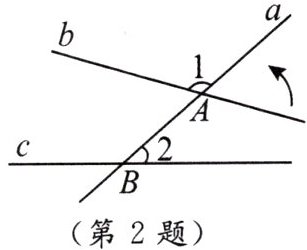
2. 如图,直线$a与直线b交于点A$,与直线$c交于点B$,$\angle 1 = 120^{\circ}$,$\angle 2 = 40^{\circ}$.要使直线$b与直线c$平行,则可将直线$b绕点A$逆时针旋转(B)

A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
]

答案： B

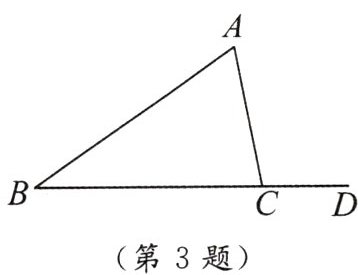
3. 如图,在$\triangle ABC$中：
(1)若$\angle A = 50^{\circ}$,$\angle ACB = 70^{\circ}$,则$\angle B = $$60°$.
(2)若$\angle A = 50^{\circ}$,$\angle B = 42^{\circ}$,则$\angle ACD = $$92°$.
]

答案：
(1) $60°$
(2) $92°$

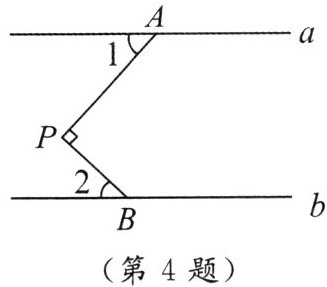
4. 如图,$a // b$,$PA \perp PB$,$\angle 1 = 35^{\circ}$,则$\angle 2$的度数是55°.
]

答案： 55°

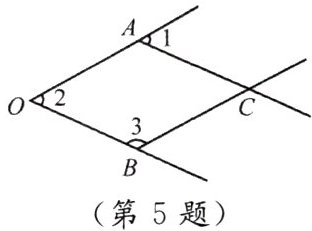
5. 如图,一个由$4$条线段构成的“鱼”形图案,其中$\angle 1 = 50^{\circ}$,$\angle 2 = 50^{\circ}$,$\angle 3 = 130^{\circ}$,找出图中的平行线,并说明理由.
]

答案： 图中的平行线为OA//BC，OB//AC。
理由如下：
1.
∵∠1=50°，∠2=50°，
∴∠1=∠2，
∴OB//AC（同位角相等，两直线平行）。
2.
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA//BC（同旁内角互补，两直线平行）。

6. 命题“若$a$是自然数,则代数式$(5a + 2)(5a + 1) + 3的值是5$的倍数.”是真命题还是假命题？如果是假命题,请说明理由；如果是真命题,请给出证明.

答案： 真命题。
证明：
$\begin{aligned}&(5a + 2)(5a + 1) + 3\\=&25a^2 + 5a + 10a + 2 + 3\\=&25a^2 + 15a + 5\\=&5(5a^2 + 3a + 1)\end{aligned}$
因为$a$是自然数，所以$5a^2 + 3a + 1$是整数，因此$5(5a^2 + 3a + 1)$是5的倍数，即代数式的值是5的倍数。