《2025年全程助学与学习评估八年级数学上册浙教版》

7. 元旦联欢会上,同学们玩抢凳子游戏,在与$A$,$B$,$C$三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将$A$,$B$,$C三名同学所在位置看作\triangle ABC$的三个顶点,那么凳子应该放在$\triangle ABC$的(D)
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点
D.三边垂直平分线的交点

答案： D

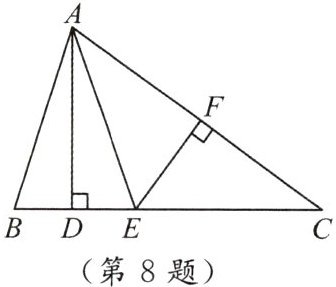
8. 如图,在$\triangle ABC$中,$AD\perp BC$,$EF垂直平分AC$,交$AC于点F$,交$BC于点E$,且$BD = DE$,连结$AE$.
(1) 求证：$AB = EC$.
(2) 若$\triangle ABC的周长为32\mathrm{cm}$,$AC = 12\mathrm{cm}$,求$DC$的长.
]

答案：
(1)见证明过程；
(2)10cm。

9. 如图 1,在四边形$ABCD$中,$AD = CD$,$AB = CB$.我们把这种两组邻边分别相等的四边形叫做“筝形”.
【性质探究】
(1) 如图 1,连结筝形$ABCD的对角线AC$,$BD交于点O$,试探究筝形$ABCD$的性质,并填空.
对角线$AC$,$BD$的位置关系是：垂直；$AO与CO$的数量关系是：AO=CO.
【知识应用】
秀秀想要做一个“筝形”风筝,她先固定中间的“十字架”,再确定四周.

(第9题)
(2) ①如图 2,从数学的角度看,秀秀确定“十字架”对角线$EG和HF$时应满足的条件是EG垂直平分HF（或HF垂直平分EG）；
②借助图 2 以及①中所写条件,说明四边形$EHGF$是个“筝形”.
② ∵EG垂直平分HF，∴EH=EF，GH=GF（线段垂直平分线上的点到线段两端点的距离相等），∴四边形EHGF是筝形。
【应用拓展】
(3) 在“筝形”风筝$EHGF$中,已知$EG = 60\mathrm{cm}$,$HF = 40\mathrm{cm}$,求“筝形”风筝$EHGF$的面积.
(3) 1200cm²

答案：
(1) 垂直；AO=CO
(2)① EG垂直平分HF（或HF垂直平分EG）
②
∵EG垂直平分HF，
∴EH=EF，GH=GF（线段垂直平分线上的点到线段两端点的距离相等），
∴四边形EHGF是筝形。
(3) 1200cm²