7. $ \triangle ABC $ 与 $ \triangle DEF $ 中,给出下列四组条件:
① $ AB = DE $,$ BC = EF $,$ AC = DF $;② $ AB = DE $,$ \angle B = \angle E $,$ BC = EF $;
③ $ \angle B = \angle E $,$ BC = EF $,$ \angle C = \angle F $;④ $ AB = DE $,$ AC = DF $,$ \angle B = \angle E $.
其中,能使 $ \triangle ABC \cong \triangle DEF $ 的条件是(
A.①③④
B.②③④
C.①②③
D.①②④
① $ AB = DE $,$ BC = EF $,$ AC = DF $;② $ AB = DE $,$ \angle B = \angle E $,$ BC = EF $;
③ $ \angle B = \angle E $,$ BC = EF $,$ \angle C = \angle F $;④ $ AB = DE $,$ AC = DF $,$ \angle B = \angle E $.
其中,能使 $ \triangle ABC \cong \triangle DEF $ 的条件是(
C
)A.①③④
B.②③④
C.①②③
D.①②④
答案:
C
8. 如图,$ AD $ 是 $ \triangle ABC $ 的中线,点 $ E,F $ 分别在 $ AB,AC $ 上(点 $ E,F $ 不与端点重合),且 $ DE \perp DF $。则 $ BE + CF $ 与 $ EF $ 的关系是(
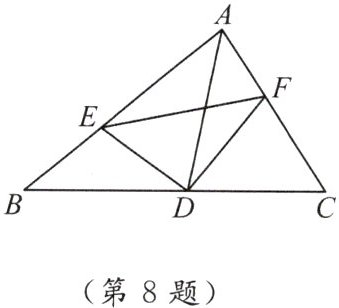
A.$ BE + CF > EF $
B.$ BE + CF < EF $
C.$ BE + CF = EF $
D.不确定
A
)
A.$ BE + CF > EF $
B.$ BE + CF < EF $
C.$ BE + CF = EF $
D.不确定
答案:
A
9. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC < BC $.
(1) 要求尺规作图,不写作法,但保留作图痕迹:①作出 $ AB $ 的垂直平分线 $ MN $ 与 $ AB $ 交于点 $ D $,与 $ BC $ 交于点 $ E $;②过点 $ B $ 作 $ BF $ 垂直于 $ AE $,垂足为 $ F $.
(2) 求证:$ AC = BF $.
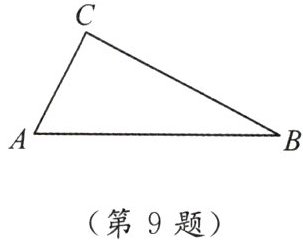
(1) 要求尺规作图,不写作法,但保留作图痕迹:①作出 $ AB $ 的垂直平分线 $ MN $ 与 $ AB $ 交于点 $ D $,与 $ BC $ 交于点 $ E $;②过点 $ B $ 作 $ BF $ 垂直于 $ AE $,垂足为 $ F $.
(2) 求证:$ AC = BF $.

答案:
(1) ①如图,作出AB的垂直平分线MN(分别以A、B为圆心,大于AB一半长为半径画弧,两弧交于两点,过两点作直线MN),交AB于D,交BC于E;②如图,过B作BF⊥AE(以B为圆心画弧交AE于两点,分别以两点为圆心画弧交于一点,过B与该点作直线BF),垂足为F。(作图痕迹保留)
(2) 证明:
∵MN是AB的垂直平分线,
∴EA=EB。
∵∠C=90°,BF⊥AE,
∴∠C=∠BFE=90°。
∵∠AEC=∠BEF,
∴∠CAE=∠FBE(等角的余角相等)。
在△ACE和△BFE中,
∠C=∠BFE,
∠CAE=∠FBE,
EA=EB,
∴△ACE≌△BFE(AAS)。
∴AC=BF。
(1) ①如图,作出AB的垂直平分线MN(分别以A、B为圆心,大于AB一半长为半径画弧,两弧交于两点,过两点作直线MN),交AB于D,交BC于E;②如图,过B作BF⊥AE(以B为圆心画弧交AE于两点,分别以两点为圆心画弧交于一点,过B与该点作直线BF),垂足为F。(作图痕迹保留)
(2) 证明:
∵MN是AB的垂直平分线,
∴EA=EB。
∵∠C=90°,BF⊥AE,
∴∠C=∠BFE=90°。
∵∠AEC=∠BEF,
∴∠CAE=∠FBE(等角的余角相等)。
在△ACE和△BFE中,
∠C=∠BFE,
∠CAE=∠FBE,
EA=EB,
∴△ACE≌△BFE(AAS)。
∴AC=BF。
10. 如图,在 $ \triangle ABC $ 中,如果 $ BD,CE $ 分别是 $ \angle ABC,\angle ACB $ 的平分线且相交于点 $ P $,设 $ \angle A = n^{\circ} $.
(1) 求 $ \angle BPC $ 的度数(用含 $ n $ 的代数式表示)。
(2) 当 $ n = 60 $ 时,求证:$ BC = CD + BE $.
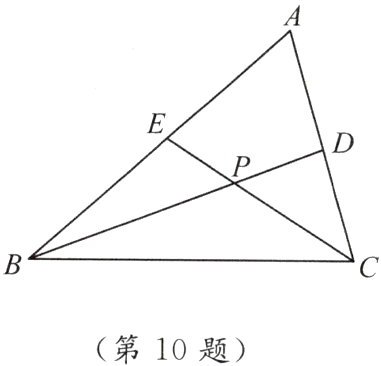
(1) 求 $ \angle BPC $ 的度数(用含 $ n $ 的代数式表示)。
(2) 当 $ n = 60 $ 时,求证:$ BC = CD + BE $.

答案:
(1) 在△ABC中,∠A = n°,则∠ABC + ∠ACB = 180° - n°。
∵BD,CE分别平分∠ABC,∠ACB,
∴∠PBC = 1/2∠ABC,∠PCB = 1/2∠ACB。
∴∠PBC + ∠PCB = 1/2(∠ABC + ∠ACB) = 1/2(180° - n°) = 90° - n°/2。
在△BPC中,∠BPC = 180° - (∠PBC + ∠PCB) = 180° - (90° - n°/2) = 90° + n°/2。
故∠BPC = (90 + n/2)°。
(2) 当n = 60时,∠A = 60°,则∠BPC = 90° + 60°/2 = 120°。
在BC上截取BF = BE,连接PF。
∵BD平分∠ABC,
∴∠EBP = ∠FBP。
又
∵BP = BP,BE = BF,
∴△EBP ≌ △FBP(SAS)。
∴∠EPB = ∠FPB。
∵∠BPC = 120°,
∴∠EPB + ∠DPC = 60°(∠EPB + ∠DPC = 180° - ∠BPC)。
由△EBP ≌ △FBP,得∠EPB = ∠FPB = 60°,
∴∠FPC = ∠BPC - ∠FPB = 120° - 60° = 60°。
∵CE平分∠ACB,
∴∠FCP = ∠DCP。
又
∵PC = PC,∠FPC = ∠DPC = 60°,
∴△FPC ≌ △DPC(ASA)。
∴FC = DC。
∵BC = BF + FC,BF = BE,FC = DC,
∴BC = BE + CD。
(1) 在△ABC中,∠A = n°,则∠ABC + ∠ACB = 180° - n°。
∵BD,CE分别平分∠ABC,∠ACB,
∴∠PBC = 1/2∠ABC,∠PCB = 1/2∠ACB。
∴∠PBC + ∠PCB = 1/2(∠ABC + ∠ACB) = 1/2(180° - n°) = 90° - n°/2。
在△BPC中,∠BPC = 180° - (∠PBC + ∠PCB) = 180° - (90° - n°/2) = 90° + n°/2。
故∠BPC = (90 + n/2)°。
(2) 当n = 60时,∠A = 60°,则∠BPC = 90° + 60°/2 = 120°。
在BC上截取BF = BE,连接PF。
∵BD平分∠ABC,
∴∠EBP = ∠FBP。
又
∵BP = BP,BE = BF,
∴△EBP ≌ △FBP(SAS)。
∴∠EPB = ∠FPB。
∵∠BPC = 120°,
∴∠EPB + ∠DPC = 60°(∠EPB + ∠DPC = 180° - ∠BPC)。
由△EBP ≌ △FBP,得∠EPB = ∠FPB = 60°,
∴∠FPC = ∠BPC - ∠FPB = 120° - 60° = 60°。
∵CE平分∠ACB,
∴∠FCP = ∠DCP。
又
∵PC = PC,∠FPC = ∠DPC = 60°,
∴△FPC ≌ △DPC(ASA)。
∴FC = DC。
∵BC = BF + FC,BF = BE,FC = DC,
∴BC = BE + CD。
查看更多完整答案,请扫码查看


