7. 若不等式组$\begin{cases}x > m,\\x \leq 2\end{cases} $无解,则$m$的取值范围是
$m\geq2$
.
答案:
【解析】:不等式组为$\begin{cases}x > m, \\ x \leq 2\end{cases}$。
若不等式组无解,则$x$的取值范围无交集,即$m \geq 2$时,$x > m$与$x \leq 2$无法同时成立。
因此,$m$的取值范围为$m \geq 2$。
【答案】:$m \geq 2$(或表示为$[2, +\infty)$的对应选项,根据题目选项形式选择)
由于题目要求填空形式,直接填写结果:
【答案】:$m\geq2$(若为选择题,根据选项对应填写)
若不等式组无解,则$x$的取值范围无交集,即$m \geq 2$时,$x > m$与$x \leq 2$无法同时成立。
因此,$m$的取值范围为$m \geq 2$。
【答案】:$m \geq 2$(或表示为$[2, +\infty)$的对应选项,根据题目选项形式选择)
由于题目要求填空形式,直接填写结果:
【答案】:$m\geq2$(若为选择题,根据选项对应填写)
▲8. 运行如图程序,规定:“从输入一个值$x到判定结果是否大于95$”为一次程序操作,如果程序操作进行了三次才停止,那么$x$的取值范围是
]
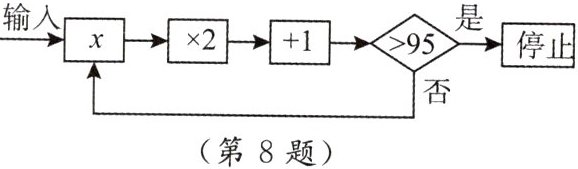
11<x≤23
.]

答案:
$11<x\leq23$(根据题目要求,若为填空题直接填此范围)
9. 已知方程组$\begin{cases}x + y = -7 - a,\\x - y = 1 + 3a\end{cases} 的解x$,$y$满足:$x$为非正数,$y$为负数.
(1) 求$a$的取值范围.
(2) 化简$\vert a - 3\vert + \vert a + 2\vert$.
(3) 在$a$的取值范围中,当$a$为何整数时,关于$x的不等式2ax + x > 2a + 1的解为x < 1$?
(1) 求$a$的取值范围.
(2) 化简$\vert a - 3\vert + \vert a + 2\vert$.
(3) 在$a$的取值范围中,当$a$为何整数时,关于$x的不等式2ax + x > 2a + 1的解为x < 1$?
答案:
(1) 解方程组
$\begin{cases}x + y = -7 - a, \\x - y = 1 + 3a.\end{cases}$
将两式相加,得到:
$2x = -6 + 2a \implies x = a - 3$
将两式相减,得到:
$2y = -8 - 4a \implies y = -4 - 2a \quad(或者由 y = -7 - a - x = -7 - a - (a - 3) = -4 - 2a 得出)$
根据$x$为非正数,$y$为负数,得到不等式组:
$\begin{cases}a - 3 \leq 0, \\-4 - 2a < 0.\end{cases}$
解不等式组,得到:
$-2 < a \leq 3$
(2)
因为$-2 < a \leq 3$,
所以$a - 3 \leq 0$,$a + 2 > 0$,
因此,
$|a - 3| + |a + 2| = 3 - a + a + 2 = 5$
(3)
不等式$2ax + x > 2a + 1$可以化简为:
$(2a + 1)x > 2a + 1$
因为不等式的解为$x < 1$,
所以$2a + 1 < 0$,
解得:
$a < -\frac{1}{2}$
结合$a$的取值范围$-2 < a \leq 3$,得到$a$的整数解为$-1$。
所以当$a = -1$时,关于$x$的不等式$2ax + x > 2a + 1$的解为$x < 1$。
(1) 解方程组
$\begin{cases}x + y = -7 - a, \\x - y = 1 + 3a.\end{cases}$
将两式相加,得到:
$2x = -6 + 2a \implies x = a - 3$
将两式相减,得到:
$2y = -8 - 4a \implies y = -4 - 2a \quad(或者由 y = -7 - a - x = -7 - a - (a - 3) = -4 - 2a 得出)$
根据$x$为非正数,$y$为负数,得到不等式组:
$\begin{cases}a - 3 \leq 0, \\-4 - 2a < 0.\end{cases}$
解不等式组,得到:
$-2 < a \leq 3$
(2)
因为$-2 < a \leq 3$,
所以$a - 3 \leq 0$,$a + 2 > 0$,
因此,
$|a - 3| + |a + 2| = 3 - a + a + 2 = 5$
(3)
不等式$2ax + x > 2a + 1$可以化简为:
$(2a + 1)x > 2a + 1$
因为不等式的解为$x < 1$,
所以$2a + 1 < 0$,
解得:
$a < -\frac{1}{2}$
结合$a$的取值范围$-2 < a \leq 3$,得到$a$的整数解为$-1$。
所以当$a = -1$时,关于$x$的不等式$2ax + x > 2a + 1$的解为$x < 1$。
10. 先阅读下面的例题,再按要求完成作业题.
例题:解一元二次不等式$(3x - 2)(2x + 1) > 0$.
解:由乘法法则“两数相乘,同号得正”可得①$\begin{cases}3x - 2 > 0,\\2x + 1 > 0\end{cases} $或②$\begin{cases}x - 2 < 0,\\2x + 1 < 0,\end{cases} $
解不等式组①得$x > \frac{2}{3}$,解不等式组②得$x < -\frac{1}{2}$.
$\therefore一元二次不等式(3x - 2)(2x + 1) > 0的解集是x > \frac{2}{3}或x < -\frac{1}{2}$.
★作业题:求不等式$\frac{5x + 1}{2x - 3} < 0$的解集.
例题:解一元二次不等式$(3x - 2)(2x + 1) > 0$.
解:由乘法法则“两数相乘,同号得正”可得①$\begin{cases}3x - 2 > 0,\\2x + 1 > 0\end{cases} $或②$\begin{cases}x - 2 < 0,\\2x + 1 < 0,\end{cases} $
解不等式组①得$x > \frac{2}{3}$,解不等式组②得$x < -\frac{1}{2}$.
$\therefore一元二次不等式(3x - 2)(2x + 1) > 0的解集是x > \frac{2}{3}或x < -\frac{1}{2}$.
★作业题:求不等式$\frac{5x + 1}{2x - 3} < 0$的解集.
答案:
由除法法则“两数相除,异号得负”可得:
① $\begin{cases}5x + 1 > 0, \\2x - 3 < 0,\end{cases}$
或②$\begin{cases}5x + 1 < 0, \\2x - 3 > 0,\end{cases}$
解不等式组①:
$5x + 1 > 0$,得$x > -\frac{1}{5}$;
$2x - 3 < 0$,得$x < \frac{3}{2}$;
综合这两个不等式,得到不等式组①的解集为$-\frac{1}{5} < x < \frac{3}{2}$。
解不等式组②:
$5x + 1 < 0$,得$x < -\frac{1}{5}$;
$2x - 3 > 0$,得$x > \frac{3}{2}$;
这两个不等式没有交集,所以不等式组②无解。
综上所述,原不等式$\frac{5x + 1}{2x - 3} < 0$的解集为$-\frac{1}{5} < x < \frac{3}{2}$。
① $\begin{cases}5x + 1 > 0, \\2x - 3 < 0,\end{cases}$
或②$\begin{cases}5x + 1 < 0, \\2x - 3 > 0,\end{cases}$
解不等式组①:
$5x + 1 > 0$,得$x > -\frac{1}{5}$;
$2x - 3 < 0$,得$x < \frac{3}{2}$;
综合这两个不等式,得到不等式组①的解集为$-\frac{1}{5} < x < \frac{3}{2}$。
解不等式组②:
$5x + 1 < 0$,得$x < -\frac{1}{5}$;
$2x - 3 > 0$,得$x > \frac{3}{2}$;
这两个不等式没有交集,所以不等式组②无解。
综上所述,原不等式$\frac{5x + 1}{2x - 3} < 0$的解集为$-\frac{1}{5} < x < \frac{3}{2}$。
查看更多完整答案,请扫码查看


