《2025年全程助学与学习评估八年级数学上册浙教版》

1. 若点 $ P(x,y) $ 的坐标满足 $ xy ＜ 0 $,则点 $ P $ 的位置在(C)
A.第一、三象限
B.第二、三象限
C.第二、四象限
D.第一、四象限

答案： C

2. 已知 $ A(4,5) $,$ B(8,5) $,则直线 $ AB $ 的位置特点是(A)
A.与 $ x $ 轴平行
B.$ AB $ 上各点的纵坐标都不相同
C.与 $ x $ 轴相交
D.与 $ y $ 轴平行

答案： A

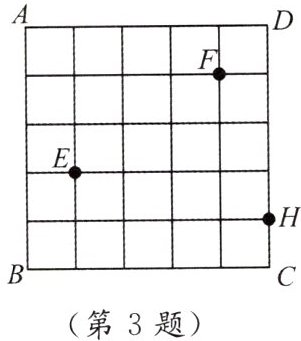
3. 如图,正方形网格 $ ABCD $ 是由 $ 25 $ 个边长相等的小正方形组成,将此网格放到一个平面直角坐标系中,使 $ BC // x $ 轴,若点 $ E $ 的坐标为 $ (-3,-1) $,则点 $ H $ 的坐标为(1,-1).
]

答案： (1,-1)

4. 在平面直角坐标系中,若一个点的横、纵坐标均为整数,则我们称该点为格点. 若格点 $ P(2m - 1,m + 2) $ 在第二象限,则 $ m $ 的值为$-1$或$0$.

答案： $-1$或$0$

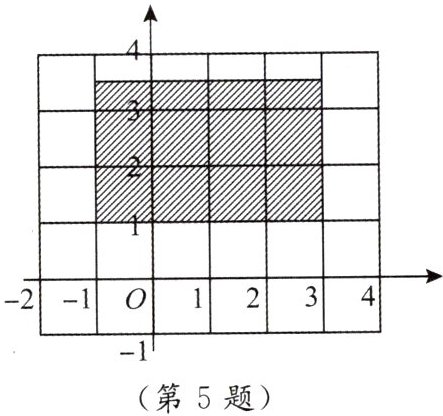
5. 已知点 $ A(2,15) $,$ B(\sqrt{5},3) $,$ C(-5,2) $,$ D(-0.5,\sqrt{7}) $. 判断这些点中,哪些在阴影区域内,哪些不在阴影区域内？
]

答案： 在阴影区域内的点：B、D；不在阴影区域内的点：A、C。
解析：
根据平面直角坐标系及阴影区域范围（x∈[-1,3]，y∈[1,3]，包含边界）：
A(2,15)：y=15＞3，不在区域内；
B(√5,3)：√5≈2.236∈[-1,3]，y=3∈[1,3]，在区域内；
C(-5,2)：x=-5＜-1，不在区域内；
D(-0.5,√7)：-0.5∈[-1,3]，√7≈2.645∈[1,3]，在区域内。
结论：在阴影区域内：B、D；不在：A、C。

6. 已知等边 $ \triangle ABC $ 的两个顶点的坐标为 $ A(-4,0) $,$ B(2,0) $,试求.
(1) 点 $ C $ 的坐标.
(2) $ \triangle ABC $ 的面积.

答案：
(1) 因为A(-4,0)，B(2,0)，所以AB在x轴上，AB的中点坐标为$(\frac{-4+2}{2},0)=(-1,0)$，AB的长度为$|2 - (-4)|=6$。
等边三角形三线合一，点C在AB的垂直平分线上，AB垂直平分线为直线$x=-1$，设C(-1,y)。
由AC=AB=6，得$\sqrt{(-1 - (-4))^2 + (y - 0)^2}=6$，即$\sqrt{3^2 + y^2}=6$，平方得$9 + y^2=36$，$y^2=27$，$y=\pm 3\sqrt{3}$。
所以点C的坐标为$(-1,3\sqrt{3})$或$(-1,-3\sqrt{3})$。
(2) $\triangle ABC$的面积为$\frac{1}{2} × AB × |y|=\frac{1}{2} × 6 × 3\sqrt{3}=9\sqrt{3}$。
(1) $(-1,3\sqrt{3})$，$(-1,-3\sqrt{3})$；
(2) $9\sqrt{3}$