1. 边长为 2 的等边三角形的面积为
$\sqrt{3}$
.
答案:
$\sqrt{3}$
2. 将一副三角尺按如图所示的方式叠放在一起,若 $ AB = 6cm $,则阴影部分的面积是

9/2
$ cm^{2} $.
答案:
9/2
3. 直角三角形一条直角边长为 12,周长为 30,则斜边上的中线长为
6.5
.
答案:
(此处应填写计算出的中线长度对应的选择,由于题目未给出选择项,直接给出数值答案的格式为)$6.5$(如果题目有选项则填写对应选项字母)。
4. 在 $ \triangle ABC $ 中, $ \angle A + \angle B = \angle C $,且 $ AC = \frac{1}{2}AB $,则 $ \angle A = $
60°
.
答案:
60°
5. 已知 $ a,b,c $ 是 $ \triangle ABC $ 的三边长,且满足 $ (a - b)^{2} + |c^{2} - a^{2} - b^{2}| = 0 $,则下列对 $ \triangle ABC $ 的形状的判断准确的为 (
A.直角三角形但非等腰三角形
B.等腰三角形或直角三角形
C.等腰直角三角形
D.等边三角形
C
)A.直角三角形但非等腰三角形
B.等腰三角形或直角三角形
C.等腰直角三角形
D.等边三角形
答案:
C
6. 如图,一棵树因雪灾于 $ A $ 处折断,测得树梢触地点 $ B $ 到树根 $ C $ 处的距离为 4 米,折断的树枝 $ AB $ 与地面 $ BC $ 的夹角为 $ 45^{\circ} $,树干 $ AC $ 垂直于地面,那么此时在未折断前的高度为多少米(精确到 0.1 米,参考值: $ \sqrt{2} \approx 1.41,\sqrt{3} \approx 1.73 $ )?
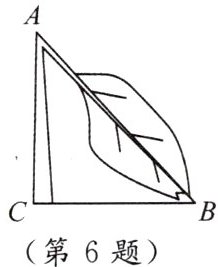

答案:
在Rt△ABC中,∠C=90°,∠B=45°,BC=4米。
∵∠B=45°,∠C=90°,
∴∠A=45°,
∴AC=BC=4米。
由勾股定理得:AB=$\sqrt{AC^2 + BC^2}$=$\sqrt{4^2 + 4^2}$=$\sqrt{32}$=4$\sqrt{2}$≈4×1.41=5.64米。
未折断前高度为AC + AB≈4 + 5.64=9.64≈9.6米。
答:未折断前的高度约为9.6米。
∵∠B=45°,∠C=90°,
∴∠A=45°,
∴AC=BC=4米。
由勾股定理得:AB=$\sqrt{AC^2 + BC^2}$=$\sqrt{4^2 + 4^2}$=$\sqrt{32}$=4$\sqrt{2}$≈4×1.41=5.64米。
未折断前高度为AC + AB≈4 + 5.64=9.64≈9.6米。
答:未折断前的高度约为9.6米。
7. 如图,等腰 $ \triangle ABC $ 中, $ AB = AC, \angle C = 30^{\circ},AB \perp AD,AD = 2 $,求 $ BC $ 的长.
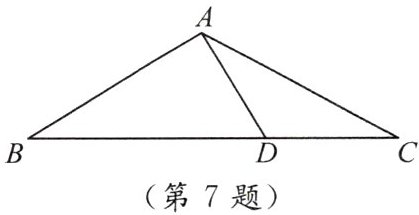

答案:
6
8. 将一副三角尺按如图所示的方式放置,点 $ C $ 在 $ FD $ 的延长线上,点 $ B $ 在 $ ED $ 上, $ AB // CF, \angle F = \angle ACB = 90^{\circ}, \angle E = 45^{\circ}, \angle A = 60^{\circ},AC = 10 $,求 $ CD $ 的长.
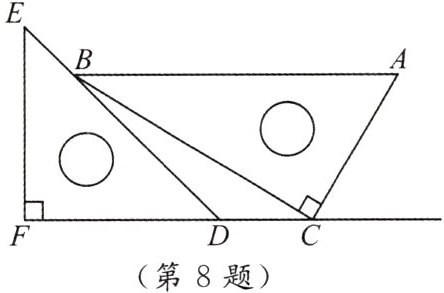

答案:
$15 - 5\sqrt{3}$
查看更多完整答案,请扫码查看


