《2025年全程助学与学习评估八年级数学上册浙教版》

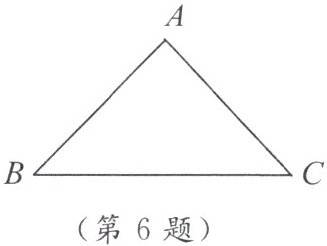
6. 如图,$ \triangle ABC $ 为等腰直角三角形,其中斜边 $ BC = 6 $.
(1) 建立适当的直角坐标系,并写出各个顶点的坐标.
(2) 若将 $ \triangle ABC $ 各顶点的纵坐标不变,横坐标都加 $ 2 $,所得三角形与原三角形的位置有何关系？

答案：
(1) 以BC的中点为原点，BC所在直线为x轴，过中点垂直于BC的直线为y轴建立直角坐标系。
∵BC=6，
∴B(-3,0)，C(3,0)。
∵△ABC为等腰直角三角形，斜边上的高为BC的一半，即3，
∴A(0,3)。
顶点坐标：A(0,3)，B(-3,0)，C(3,0)。
(2) 所得三角形是原三角形向右平移2个单位得到的。

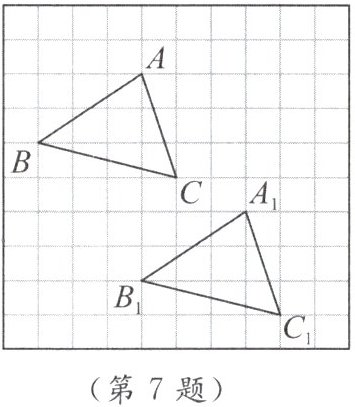
7. 在方格纸中,把一个图形先沿水平方向平移 $ |a| $ 格(当 $ a $ 为正数时,表示向右平移；当 $ a $ 为负数时,表示向左平移),再沿竖直方向平移 $ |b| $ 格(当 $ b $ 为正数时,表示向上平移；当 $ b $ 为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为 $ [a,b] $. 例如,把如图所示的 $ \triangle ABC $ 先向右平移 $ 3 $ 格,再向下平移 $ 4 $ 格得到 $ \triangle A_1B_1C_1 $,可以把这个过程记为 $ [3,-4] $. 若再将 $ \triangle A_1B_1C_1 $ 经过 $ [5,2] $ 得到 $ \triangle A_2B_2C_2 $,则 $ \triangle ABC $ 经过平移得到 $ \triangle A_2B_2C_2 $ 的过程是(B)

A.$ [2,6] $
B.$ [8,-2] $
C.$ [8,-6] $
D.$ [-8,-1] $

答案： B

▲8. 在平面直角坐标系中,规定一个点先向上平移 $ 2 $ 个单位,再向右平移 $ 1 $ 个单位为 $ 1 $ 次运动. 则点 $ P(-2,-3) $ 经过6次这样的运动后到达点 $ P'(4,9) $.

答案： 6

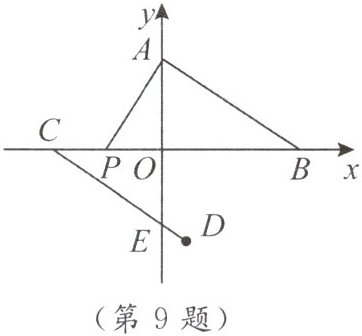
9. 如图,已知点 $ A(0,2) $,平移线段 $ AB $,将点 $ A $ 平移到点 $ C(-3,0) $,点 $ B $ 平移到点 $ D(1,-2) $,$ CD $ 交 $ y $ 轴于点 $ E $.
(1) 求点 $ B $ 的坐标.
★(2) $ P $ 为 $ x $ 轴上一动点,若 $ S_{\triangle ABP} = 5 $,求点 $ P $ 的坐标.

答案：
(1) 设点$ B $的坐标为$(x,y)$。
∵ 线段$ AB $平移后得到线段$ CD $，点$ A(0,2) $平移到点$ C(-3,0) $，
∴ 平移向量为$(-3-0,0-2)=(-3,-2)$。
∵ 点$ B $平移到点$ D(1,-2) $，
∴ $ x-3=1 $，$ y-2=-2 $，
解得$ x=4 $，$ y=0 $。
∴ 点$ B $的坐标为$(4,0)$。
(2) 设点$ P $的坐标为$(p,0)$（$ P $在$ x $轴上）。
∵ $ A(0,2) $，$ B(4,0) $，$ P(p,0) $，
∴ $ \triangle ABP $的底边$ BP=|p-4| $，高为点$ A $到$ x $轴的距离，即$ 2 $。
由$ S_{\triangle ABP}=5 $，得$\frac{1}{2} × |p-4| × 2=5$，
化简得$|p-4|=5$，
∴ $ p-4=5 $或$ p-4=-5 $，
解得$ p=9 $或$ p=-1 $。
∴ 点$ P $的坐标为$(9,0)$或$(-1,0)$。
(1) $(4,0)$
(2) $(9,0)$或$(-1,0)$