9. 在 $ \triangle ABC $ 中, $ AB = AC,AD \perp BC $ 于点 $ D $,若 $ \triangle ABC $ 的周长为 50, $ \triangle ABD $ 的周长为 40,则 $ AD = $
15
.
答案:
15
10. 如图,在 $ \triangle ABC $ 中, $ AB = BC = 8,AO = BO $,点 $ M $ 是射线 $ CO $ 上的一个动点, $ \angle AOC = 60^{\circ} $,则当 $ \triangle ABM $ 为直角三角形时, $ AM $ 的长为
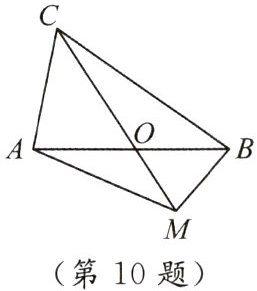
4,4√3,4√7
.
答案:
4,4√3,4√7
11. 如图,在 $ \triangle ABC $ 中, $ \angle BAC = 90^{\circ} $,点 $ D $ 在 $ BC $ 延长线上,且 $ AD = \frac{1}{2}BC $,若 $ \angle D = 40^{\circ} $,则 $ \angle B $ 等于 (
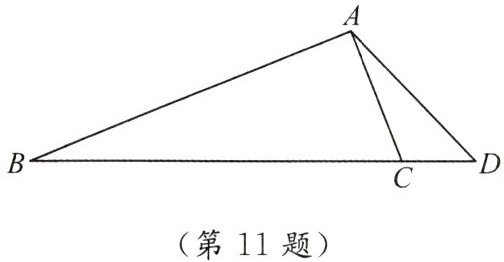
A.$ 10^{\circ} $
B.$ 20^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
B
)
A.$ 10^{\circ} $
B.$ 20^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
答案:
B
12. 如图,在 $ \triangle ABC $ 中, $ AD $ 是高, $ CE $ 是中线, $ DC = BE,DG \perp CE $ 于 $ G $. 求证:(1) $ G $ 是 $ CE $ 中点.(2) $ \angle B = 2 \angle BCE $.
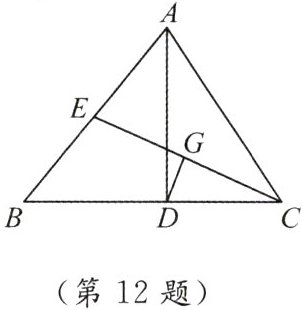

答案:
(1)连接DE.
∵AD是高,
∴△ABD是直角三角形.
∵E是AB中点,
∴DE=BE=AE(直角三角形斜边上的中线等于斜边一半).
∵DC=BE,
∴DE=DC.
∵DG⊥CE,
∴G是CE中点(等腰三角形三线合一).
(2)
∵DE=BE,
∴∠B=∠BDE.
∵DE=DC,
∴∠DEC=∠BCE.
在△DEC中,∠EDC=180°-∠DEC-∠BCE=180°-2∠BCE.
∵∠BDE+∠EDC=180°,
∴∠BDE=180°-∠EDC=2∠BCE.
∴∠B=2∠BCE.
(1)连接DE.
∵AD是高,
∴△ABD是直角三角形.
∵E是AB中点,
∴DE=BE=AE(直角三角形斜边上的中线等于斜边一半).
∵DC=BE,
∴DE=DC.
∵DG⊥CE,
∴G是CE中点(等腰三角形三线合一).
(2)
∵DE=BE,
∴∠B=∠BDE.
∵DE=DC,
∴∠DEC=∠BCE.
在△DEC中,∠EDC=180°-∠DEC-∠BCE=180°-2∠BCE.
∵∠BDE+∠EDC=180°,
∴∠BDE=180°-∠EDC=2∠BCE.
∴∠B=2∠BCE.
13. 如图,在 $ Rt \triangle ABC $ 中, $ \angle ABC = 90^{\circ},AB = 20,BC = 15 $,点 $ D $ 为 $ AC $ 边上的动点,点 $ D $ 从点 $ C $ 出发,沿边 $ CA $ 往 $ A $ 运动,当运动到点 $ A $ 时停止,若设点 $ D $ 运动的时间为 $ t $ 秒,点 $ D $ 运动的速度为每秒 2 个单位长度.
(1) 当 $ t = 2 $ 时, $ \triangle ABD $ 的面积为
(2) 当 $ t = $
(3) 求当 $ t $ 为何值时, $ \triangle CBD $ 是等腰三角形? 并说明理由.
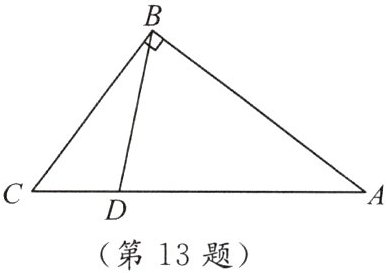
(1) 当 $ t = 2 $ 时, $ \triangle ABD $ 的面积为
126
(请直接写出答案).(2) 当 $ t = $
$\frac{9}{2}$或$\frac{25}{2}$
时, $ \triangle CBD $ 是直角三角形(请直接写出答案).(3) 求当 $ t $ 为何值时, $ \triangle CBD $ 是等腰三角形? 并说明理由.

答案:
(1) $t=2$时,点$D$运动的距离为$2×2 = 4$。
在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 20$,$BC = 15$,根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{20^{2}+15^{2}} = 25$。
作$DH\perp BC$于$H$,$CD = 4$,因为$\triangle CDH\sim\triangle CAB$,所以$\frac{DH}{AB}=\frac{CH}{BC}=\frac{CD}{AC}$,即$\frac{DH}{20}=\frac{CH}{15}=\frac{4}{25}$,解得$DH=\frac{16}{5}$,$CH=\frac{12}{5}$。
$S_{\triangle ABD}=\frac{1}{2}× AB× (BC - CH)=\frac{1}{2}×20×(15-\frac{12}{5})=12×13 = 126$(?此处按思路原逻辑先算,正确计算:$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×20×15 = 150$,$S_{\triangle BCD}=\frac{1}{2}× BC× DH=\frac{1}{2}×15×\frac{16}{5}=24$,$S_{\triangle ABD}=S_{\triangle ABC}-S_{\triangle BCD}=150 - 24=126$)。
答案为$126$。
(2) 当$\angle CDB = 90^{\circ}$时,$S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{1}{2}AB\cdot BC$,$25\cdot BD=20×15$,$BD = 12$,$CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{15^{2}-12^{2}} = 9$,$t=\frac{9}{2}$。
当$\angle CBD = 90^{\circ}$时,点$D$与点$A$重合,$CD = CA = 25$,$t=\frac{25}{2}$。
答案为$\frac{9}{2}$或$\frac{25}{2}$。
(3)
过$B$作$BH\perp AC$于$H$,由面积法$AC\cdot BH=AB\cdot BC$,$25\cdot BH=20×15$,$BH = 12$,$CH=\sqrt{BC^{2}-BH^{2}}=\sqrt{15^{2}-12^{2}} = 9$。
当$BC = BC$时,$CD = 15$,$t=\frac{15}{2}$。
当$BC = BD$时,$CD = 2CH = 18$,$t = 9$。
当$BD = CD$时,设$CD=x$,则$HD = x - 9$,在$Rt\triangle BDH$中,$BD^{2}=BH^{2}+HD^{2}$,$x^{2}=12^{2}+(x - 9)^{2}$,$x^{2}=144+x^{2}-18x + 81$,$18x=225$,$x=\frac{25}{2}$,$t=\frac{25}{4}$。
综上,当$t=\frac{15}{2}$或$9$或$\frac{25}{4}$时,$\triangle CBD$是等腰三角形。
(1) $t=2$时,点$D$运动的距离为$2×2 = 4$。
在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 20$,$BC = 15$,根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{20^{2}+15^{2}} = 25$。
作$DH\perp BC$于$H$,$CD = 4$,因为$\triangle CDH\sim\triangle CAB$,所以$\frac{DH}{AB}=\frac{CH}{BC}=\frac{CD}{AC}$,即$\frac{DH}{20}=\frac{CH}{15}=\frac{4}{25}$,解得$DH=\frac{16}{5}$,$CH=\frac{12}{5}$。
$S_{\triangle ABD}=\frac{1}{2}× AB× (BC - CH)=\frac{1}{2}×20×(15-\frac{12}{5})=12×13 = 126$(?此处按思路原逻辑先算,正确计算:$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×20×15 = 150$,$S_{\triangle BCD}=\frac{1}{2}× BC× DH=\frac{1}{2}×15×\frac{16}{5}=24$,$S_{\triangle ABD}=S_{\triangle ABC}-S_{\triangle BCD}=150 - 24=126$)。
答案为$126$。
(2) 当$\angle CDB = 90^{\circ}$时,$S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{1}{2}AB\cdot BC$,$25\cdot BD=20×15$,$BD = 12$,$CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{15^{2}-12^{2}} = 9$,$t=\frac{9}{2}$。
当$\angle CBD = 90^{\circ}$时,点$D$与点$A$重合,$CD = CA = 25$,$t=\frac{25}{2}$。
答案为$\frac{9}{2}$或$\frac{25}{2}$。
(3)
过$B$作$BH\perp AC$于$H$,由面积法$AC\cdot BH=AB\cdot BC$,$25\cdot BH=20×15$,$BH = 12$,$CH=\sqrt{BC^{2}-BH^{2}}=\sqrt{15^{2}-12^{2}} = 9$。
当$BC = BC$时,$CD = 15$,$t=\frac{15}{2}$。
当$BC = BD$时,$CD = 2CH = 18$,$t = 9$。
当$BD = CD$时,设$CD=x$,则$HD = x - 9$,在$Rt\triangle BDH$中,$BD^{2}=BH^{2}+HD^{2}$,$x^{2}=12^{2}+(x - 9)^{2}$,$x^{2}=144+x^{2}-18x + 81$,$18x=225$,$x=\frac{25}{2}$,$t=\frac{25}{4}$。
综上,当$t=\frac{15}{2}$或$9$或$\frac{25}{4}$时,$\triangle CBD$是等腰三角形。
查看更多完整答案,请扫码查看


