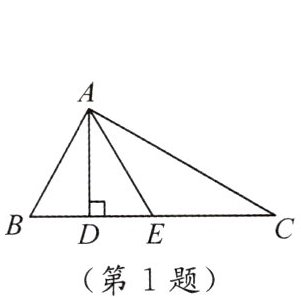
1. 如图,在△ABC中,∠BAC= 90°,AD是BC边上的高,E是BC的中点,连结AE,则图中的直角三角形共有(
A.2个
B.3个
C.4个
D.5个
]
C
)
A.2个
B.3个
C.4个
D.5个
]
答案:
C
2. 在△ABC中,满足下列条件:①∠A= 60°,∠C= 30°;②∠A+∠B= ∠C;③∠A∶∠B∶∠C= 3∶4∶5;④∠A= 90°-∠C. 其中能确定△ABC是直角三角形的有(
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
C
3. 已知等腰直角三角形的斜边长为8,则该三角形的面积为
16
.
答案:
16
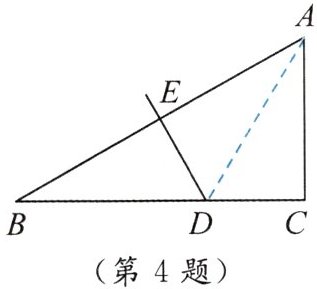
4. 如图,在△ABC中,∠C= 90°,∠B= 30°,AB的垂直平分线ED交AB于点E,交BC于点D. 若CD= 3,则BD的长为
]
6
.]

答案:
6
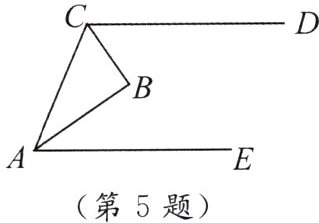
5. 如图,已知CD//AE,∠DCA与∠CAE的平分线相交于点B. 判断△ABC是否直角三角形,并证明你的结论.
]
]

答案:
△ABC是直角三角形。
证明:
∵CD//AE(已知),
∴∠DCA + ∠CAE = 180°(两直线平行,同旁内角互补)。
∵CB平分∠DCA,AB平分∠CAE(已知),
∴∠BCA = 1/2∠DCA,∠BAC = 1/2∠CAE(角平分线定义)。
∴∠BCA + ∠BAC = 1/2(∠DCA + ∠CAE) = 1/2×180° = 90°。
在△ABC中,∠ABC = 180° - (∠BCA + ∠BAC) = 180° - 90° = 90°(三角形内角和定理)。
∴△ABC是直角三角形。
证明:
∵CD//AE(已知),
∴∠DCA + ∠CAE = 180°(两直线平行,同旁内角互补)。
∵CB平分∠DCA,AB平分∠CAE(已知),
∴∠BCA = 1/2∠DCA,∠BAC = 1/2∠CAE(角平分线定义)。
∴∠BCA + ∠BAC = 1/2(∠DCA + ∠CAE) = 1/2×180° = 90°。
在△ABC中,∠ABC = 180° - (∠BCA + ∠BAC) = 180° - 90° = 90°(三角形内角和定理)。
∴△ABC是直角三角形。
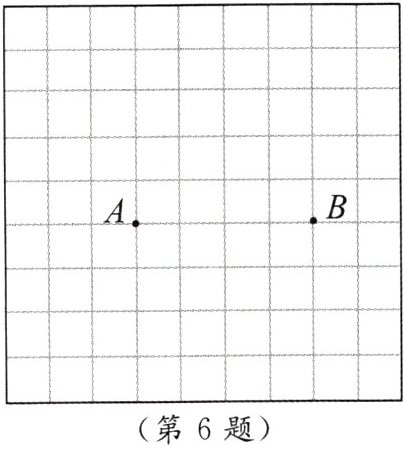
6. 在图中找出所有的格点C,使△ABC为等腰直角三角形,并指出这样的点C有几个(格点:图案中小正方形的顶点叫作格点)?
]
]

答案:
设每个小正方形的边长为1,以A为原点,水平方向为x轴,竖直方向为y轴建立直角坐标系,则$A(0,0)$,$B(4,2)$。
设点$C$的坐标为$(x,y)$。
当$\angle A$为直角时:
$AB$的水平位移为4,竖直位移为2,则$AC$需满足水平位移的平方加竖直位移的平方等于$AB$位移平方($AB^{2}=20$),且$AC$的水平位移与竖直位移乘积等于$AC$或$AB$构成正方形面积的一半(即$\frac{1}{2}×$两直角边乘积,这里两直角边平方和为20,乘积为$xy$形式,通过$x^{2}+y^{2}=20$与$2xy = \frac{1}{2}×$(以$AB$为斜边求的两直角边乘积的2倍等关系推导),实际根据等腰直角三角形两直角边相等且$AC^{2}=2AC_{x}^{2}$等关系可得:
$AC$的水平位移$x$,竖直位移$y$满足$x^{2}+y^{2}=AC^{2}$,且$AC = \frac{AB}{\sqrt{2}}=\sqrt{10}×\sqrt{2}=\sqrt{20}$的构成条件,即$x^{2}+y^{2}=20$的整数解且满足等腰直角(两方向位移绝对值相等),此时$x = 0$,$y = 0$(与A重合舍去)或$x = 2$,$y = - 2$或$x=-2$,$y = 2$等情况中符合格点的,经检验$(2,-2)$,$( - 2,2)$满足(通过计算距离和斜率验证等腰直角),同时还有$(0,4)$($AC$水平0,竖直4,$AC^{2}=16$,$AC$与$AB$构成的角通过斜率乘积为-1等验证为直角且$AC$中点到A与B到A的向量关系等验证等腰),$(4,0)$(同理),$(0,0)$舍去,所以有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$ 4个点。
当$\angle B$为直角时:
同理,以B为直角顶点,$BC$与$BA$构成等腰直角,$BA$水平位移 - 4,竖直位移 - 2,则$BC$需满足类似关系,可得$C$点:$(2,6)$,$(6,4)$,$(4,0)$(与前面重复在$\angle A$为直角时已算但在此情况也满足),$(8,2)$,经检验$(2,6)$,$(6,4)$,$(8,2)$新满足,$(4,0)$重复,所以新增3个点(除去重复)。
当$\angle C$为直角时:
设$C(x,y)$,则$AC^{2}=x^{2}+y^{2}$,$BC^{2}=(x - 4)^{2}+(y - 2)^{2}$,$AB^{2}=20$,且$AC = BC$,$AC^{2}+BC^{2}=AB^{2}$(等腰直角三角形性质),由$AC = BC$得$x^{2}+y^{2}=(x - 4)^{2}+(y - 2)^{2}$,展开$x^{2}+y^{2}=x^{2}-8x + 16+y^{2}-4y + 4$,化简得$2x+y=5$;由$AC^{2}+BC^{2}=AB^{2}$得$2(x^{2}+y^{2})=20$,即$x^{2}+y^{2}=10$。
联立$\begin{cases}2x + y=5\\x^{2}+y^{2}=10\end{cases}$,将$y = 5 - 2x$代入$x^{2}+y^{2}=10$得$x^{2}+(5 - 2x)^{2}=10$,$x^{2}+25-20x + 4x^{2}=10$,$5x^{2}-20x+15 = 0$,$x^{2}-4x + 3=0$,$(x - 1)(x - 3)=0$,解得$x = 1$,$y = 3$或$x = 3$,$y=-1$,即$(1,3)$,$(3,-1)$。
综合以上三种情况,除去重复的$(4,0)$,满足条件的$C$点有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$,$(2,6)$,$(6,4)$,$(8,2)$,$(1,3)$,$(3,-1)$,共10个点。
故答案为:满足条件的格点$C$有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$,$(2,6)$,$(6,4)$,$(8,2)$,$(1,3)$,$(3,-1)$,共10个。
设点$C$的坐标为$(x,y)$。
当$\angle A$为直角时:
$AB$的水平位移为4,竖直位移为2,则$AC$需满足水平位移的平方加竖直位移的平方等于$AB$位移平方($AB^{2}=20$),且$AC$的水平位移与竖直位移乘积等于$AC$或$AB$构成正方形面积的一半(即$\frac{1}{2}×$两直角边乘积,这里两直角边平方和为20,乘积为$xy$形式,通过$x^{2}+y^{2}=20$与$2xy = \frac{1}{2}×$(以$AB$为斜边求的两直角边乘积的2倍等关系推导),实际根据等腰直角三角形两直角边相等且$AC^{2}=2AC_{x}^{2}$等关系可得:
$AC$的水平位移$x$,竖直位移$y$满足$x^{2}+y^{2}=AC^{2}$,且$AC = \frac{AB}{\sqrt{2}}=\sqrt{10}×\sqrt{2}=\sqrt{20}$的构成条件,即$x^{2}+y^{2}=20$的整数解且满足等腰直角(两方向位移绝对值相等),此时$x = 0$,$y = 0$(与A重合舍去)或$x = 2$,$y = - 2$或$x=-2$,$y = 2$等情况中符合格点的,经检验$(2,-2)$,$( - 2,2)$满足(通过计算距离和斜率验证等腰直角),同时还有$(0,4)$($AC$水平0,竖直4,$AC^{2}=16$,$AC$与$AB$构成的角通过斜率乘积为-1等验证为直角且$AC$中点到A与B到A的向量关系等验证等腰),$(4,0)$(同理),$(0,0)$舍去,所以有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$ 4个点。
当$\angle B$为直角时:
同理,以B为直角顶点,$BC$与$BA$构成等腰直角,$BA$水平位移 - 4,竖直位移 - 2,则$BC$需满足类似关系,可得$C$点:$(2,6)$,$(6,4)$,$(4,0)$(与前面重复在$\angle A$为直角时已算但在此情况也满足),$(8,2)$,经检验$(2,6)$,$(6,4)$,$(8,2)$新满足,$(4,0)$重复,所以新增3个点(除去重复)。
当$\angle C$为直角时:
设$C(x,y)$,则$AC^{2}=x^{2}+y^{2}$,$BC^{2}=(x - 4)^{2}+(y - 2)^{2}$,$AB^{2}=20$,且$AC = BC$,$AC^{2}+BC^{2}=AB^{2}$(等腰直角三角形性质),由$AC = BC$得$x^{2}+y^{2}=(x - 4)^{2}+(y - 2)^{2}$,展开$x^{2}+y^{2}=x^{2}-8x + 16+y^{2}-4y + 4$,化简得$2x+y=5$;由$AC^{2}+BC^{2}=AB^{2}$得$2(x^{2}+y^{2})=20$,即$x^{2}+y^{2}=10$。
联立$\begin{cases}2x + y=5\\x^{2}+y^{2}=10\end{cases}$,将$y = 5 - 2x$代入$x^{2}+y^{2}=10$得$x^{2}+(5 - 2x)^{2}=10$,$x^{2}+25-20x + 4x^{2}=10$,$5x^{2}-20x+15 = 0$,$x^{2}-4x + 3=0$,$(x - 1)(x - 3)=0$,解得$x = 1$,$y = 3$或$x = 3$,$y=-1$,即$(1,3)$,$(3,-1)$。
综合以上三种情况,除去重复的$(4,0)$,满足条件的$C$点有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$,$(2,6)$,$(6,4)$,$(8,2)$,$(1,3)$,$(3,-1)$,共10个点。
故答案为:满足条件的格点$C$有$(2,-2)$,$( - 2,2)$,$(0,4)$,$(4,0)$,$(2,6)$,$(6,4)$,$(8,2)$,$(1,3)$,$(3,-1)$,共10个。
查看更多完整答案,请扫码查看


