《2025年全程助学与学习评估八年级数学上册浙教版》

7. 在△ABC中,三边长分别为a,b,c,且都是整数,若b＞a＞c,b= 5,则满足条件的三角形的个数为(A)
A.2个
B.3个
C.4个
D.5个

答案： A

8. 一个木工师傅现有两根木条,它们长分别为50cm,70cm,要选择第三根木条,钉成一个三角形木架,设第三根木条为xcm,则x的取值范围是20＜x＜120.

答案： $20＜x＜120$（填写范围即可，根据要求不填具体内容形式）

9. 已知三角形的两边长分别为5cm和2cm.
(1)如果这个三角形的第三边长为偶数,求它的第三边的长以及它的周长.
(2)如果这个三角形的周长为偶数,求它的第三边的长以及它的周长.

答案： （1）
设第三边长为$x$ $cm$，根据三角形三边关系，有：
$5 - 2 \lt x \lt 5 + 2$，
即：
$3 \lt x \lt 7$，
因为第三边长是偶数，所以：
$x = 4$或$6$。
当$x = 4$时，周长为：
$5 + 2 + 4 = 11(cm)$；
当$x = 6$时，周长为：
$5 + 2 + 6 = 13(cm)$。
所以第三边的长为$4cm$或$6cm$，周长为$11cm$或$13cm$。
（2）
设第三边长为$x$ $cm$，周长为$l$ $cm$，由三角形三边关系知：
$3 \lt x \lt 7$，
因为周长$l = 5 + 2 + x = 7 + x$为偶数，所以：
$x$必须为奇数，
因此$x = 5$。
此时周长$l = 7 + 5 = 12(cm)$。
所以第三边的长为$5cm$，周长为$12cm$。

10. (1)如图1,从A经B到C是一条柏油马路,AC是一条小路,人们从A到C,为什么不走柏油路,而喜欢走小路？请你用学过的知识解释一下原因.
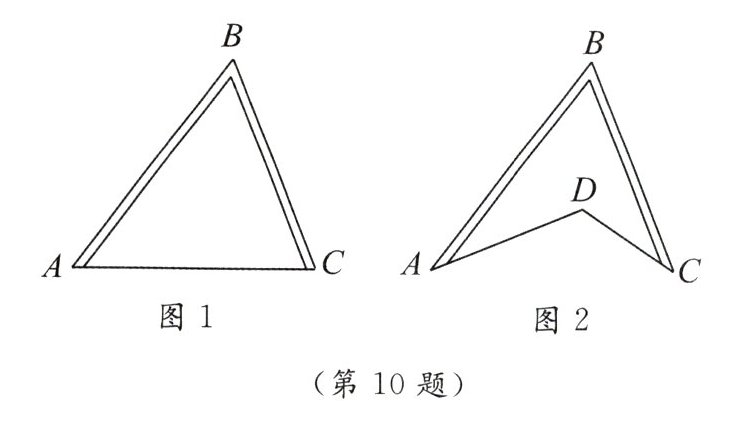
(2)如图2,从A经B到C是一条柏油马路,由A经D到C是一条小路,人们从A步行到C,为什么不走柏油路,而喜欢走小路？请你用学过的知识解释一下原因.

答案： （1）从$A$到$B$到$C$是一条柏油马路，$A$到$C$是一条小路，在图1中，$A$、$B$、$C$三点构成一个三角形。
根据三角形三边关系，对于任意三角形，任意两边之和大于第三边，即$AB + BC＞AC$，但$AC$是两点之间的直线段，$AB + BC$是绕过$B$点的路径长度。
从$A$到$C$走小路$AC$，其长度就是$AC$的长度；走柏油路从$A$经$B$到$C$，其长度是$AB + BC$。
因为两点之间线段最短，所以$AC＜AB + BC$，人们从$A$到$C$喜欢走小路是因为小路$AC$的长度更短。
（2）从$A$经$B$到$C$是一条柏油马路，从$A$经$D$到$C$是一条小路，在图2中，取$AC$上一点$D^{\prime}$（假设$D$在三角形内的情况通过转化到边上分析）。
根据三角形三边关系，在$\triangle ABD^{\prime}$和$\triangle CD^{\prime}D$（通过构造辅助点将路径转化到以$AC$为边的相关三角形中）等相关三角形中，$AD + DC$（小路长度）与$AB + BC$（柏油路长度）比较。
同样依据两点之间线段最短，$A$到$C$的直线距离是最短的，走小路$A$经$D$到$C$的整体路径长度小于走柏油路$A$经$B$到$C$的长度，即$AD + DC＜AB + BC$。
所以人们从$A$到$C$喜欢走小路是因为小路的长度更短。
故答案为：（1）因为两点之间线段最短，小路$AC$是$A$、$C$两点之间的线段，其长度小于绕过$B$点的柏油路长度$AB + BC$，所以人们喜欢走小路；（2）因为两点之间线段最短，小路$A$经$D$到$C$的整体长度小于绕过$B$点的柏油路长度$AB + BC$，所以人们喜欢走小路。