《2025年全程助学与学习评估八年级数学上册浙教版》

6. 如图,已知$AD = AC$,请找出$\triangle ABC与\triangle ABD$相等的边和角.请思考并回答下列问题：如果两个三角形有两条边和一个角对应相等,这样的两个三角形一定全等吗？

答案： 相等的边和角：
边：$AB = AB$（公共边），$AC = AD$（已知）；
角：$\angle ABC = \angle ABD$（公共角）。
结论：
如果两个三角形有两条边和一个角对应相等，这样的两个三角形不一定全等。

7. 如图,$BE \perp AC于点D$,且$AD = CD$,$BD = ED$,若$∠ABC = 54^{\circ}$,则$∠E$等于(B)

A.$25^{\circ}$
B.$27^{\circ}$
C.$30^{\circ}$
D.$45^{\circ}$

答案： B

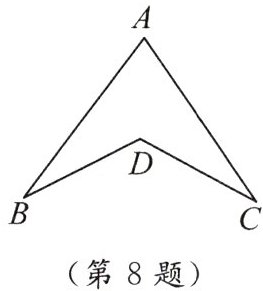
▲8. 如图,若$AB = AC$,$BD = CD$,$∠B = 20^{\circ}$,$∠BDC = 120^{\circ}$,则$∠A = $80°.

答案： 80°

★9. 如图,在$\triangle ABC$中,$AB = 5$,$AC = 3$,求$BC边上的中线AD$的取值范围.

答案： 延长AD至点E，使DE=AD，连接BE。
∵AD是BC边上的中线，
∴BD=CD。
在△ADC和△EDB中，
$\left\{\begin{array}{l} CD=BD \\ ∠ADC=∠EDB \\ AD=ED\end{array}\right.$
∴△ADC≌△EDB(SAS)，
∴BE=AC=3。
在△ABE中，AB=5，BE=3，
根据三角形三边关系：AB - BE ＜ AE ＜ AB + BE，
即5 - 3 ＜ AE ＜ 5 + 3，
∴2 ＜ AE ＜ 8。
∵AE=AD + DE=2AD，
∴2 ＜ 2AD ＜ 8，
∴1 ＜ AD ＜ 4。
结论：AD的取值范围是1 ＜ AD ＜ 4。

10. (1)画$\triangle ABC$,使$∠A = 30^{\circ}$,$AC = 3cm$,$BC = 2cm$.
(2)符合(1)中条件的三角形可以画几个？如果两个三角形有两条边和一个角对应相等,这样的两个三角形一定全等吗？

答案：
(1)
画射线$AM$；
在$AM$上取点$A$，用圆规截取$AC = 3cm$，确定点$C$；
在$C$处作射线$CN$与$AM$夹角为$30^{\circ}$；
以$C$为圆心，$2cm$为半径作弧交$CN$（若相交），设交点为$B$（有$0$个、$1$个或$2$个交点情况）；
连接$AB$，$\triangle ABC$即为所求作三角形（当有交点时）。
(2)
可以画$0$个，$1$个或$2$个；
不一定全等。