1. 如图,点 $ B,F,C,E $ 在一条直线上,$ AB // ED $,$ AC // FD $,那么添加下列一个条件后,仍无法判定 $ \triangle ABC \cong \triangle DEF $ 的是(
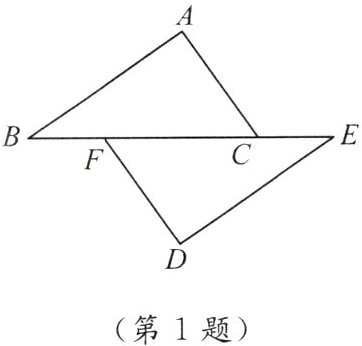
A.$ \angle A = \angle D $
B.$ AC = DF $
C.$ AB = ED $
D.$ BF = EC $
A
)
A.$ \angle A = \angle D $
B.$ AC = DF $
C.$ AB = ED $
D.$ BF = EC $
答案:
A
2. 如图,$ \triangle ADB \cong \triangle ECB $,$ \angle CBD = 40^{\circ} $,$ BD \perp EC $,则 $ \angle D $ 的度数为
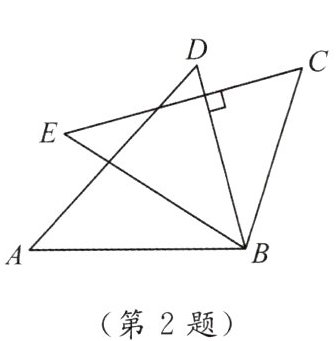
50°
.
答案:
50°
3. 如图,$ AD $ 是 $ \triangle ABC $ 的角平分线,$ DE \perp AB $ 于点 $ E $,$ S_{\triangle ABC} = 7 $,$ DE = 2 $,$ AB = 4 $,则 $ AC $ 的长是(
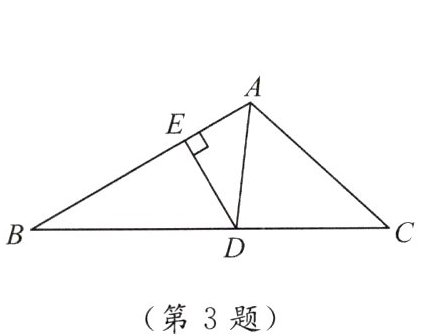
A.$ 3 $
B.$ 4 $
C.$ 6 $
D.$ 5 $
A
)
A.$ 3 $
B.$ 4 $
C.$ 6 $
D.$ 5 $
答案:
A
4. 如图,$ AB = AC $,$ AD = AE $,$ \angle BAC = \angle DAE $,$ \angle 1 = 25^{\circ} $,$ \angle 2 = 30^{\circ} $,连结 $ BE $,点 $ D $ 恰好在 $ BE $ 上,则 $ \angle 3 = $(
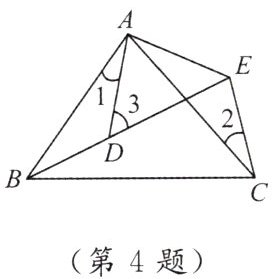
A.$ 60^{\circ} $
B.$ 55^{\circ} $
C.$ 50^{\circ} $
D.无法计算
B
)
A.$ 60^{\circ} $
B.$ 55^{\circ} $
C.$ 50^{\circ} $
D.无法计算
答案:
B
5. 如图,点 $ A,B,C,D $ 在一条直线上,$ AB = CD $,$ \angle A = \angle FBD $,$ CE // DF $。求证:$ CE = DF $.
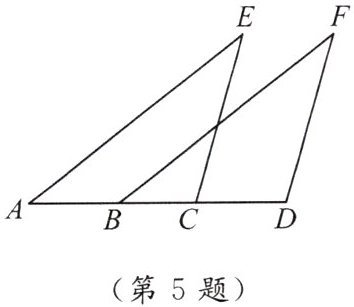

答案:
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD。
∵CE//DF,
∴∠ACE=∠D。
在△ACE和△BDF中,
∠A=∠FBD,
AC=BD,
∠ACE=∠D,
∴△ACE≌△BDF(ASA),
∴CE=DF。
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD。
∵CE//DF,
∴∠ACE=∠D。
在△ACE和△BDF中,
∠A=∠FBD,
AC=BD,
∠ACE=∠D,
∴△ACE≌△BDF(ASA),
∴CE=DF。
6. 如图,已知 $ AB = BC $,$ AB \perp BC $,$ AE \perp BD $ 于点 $ E $,$ CD \perp BD $ 于点 $ D $.
(1) 猜想线段 $ DE,AE,CD $ 的数量关系,并证明.
(2) 若 $ AE = 6 $,求 $ \triangle ABD $ 的面积.
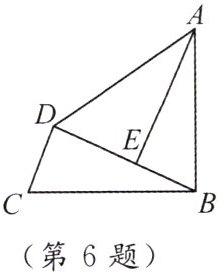
(1) 猜想线段 $ DE,AE,CD $ 的数量关系,并证明.
(2) 若 $ AE = 6 $,求 $ \triangle ABD $ 的面积.

答案:
(1) DE=AE+CD;
(2) 18.
(1) DE=AE+CD;
(2) 18.
查看更多完整答案,请扫码查看


