《2025年状元成才路创优作业100分六年级数学上册人教版湖南专版》

1. (1) 在圆形花圃的周围围上一圈篱笆,求篱笆的长,就是求圆形花圃的(周长)。如果花圃的直径是10m,那么篱笆的长是(31.4)m。
(2) 把圆规的两脚张开4cm画一个圆,这个圆的周长是(25.12)cm。如果在这个圆上每隔5cm画一个☆,大约要画(5)个☆。
(3) 圆的直径增加2cm,它的周长增加(6.28)cm；圆的半径增加2cm,它的周长增加(12.56)cm。

答案： 1.
(1)周长 31.4
(2)25.12 5
(3)6.28 12.56

(1) 下列说法正确的是(C)。
A.圆的周长是直径的3.14倍
B.大圆的圆周率比小圆的圆周率大
C.半径不相等的两个圆,周长一定不相等
D.半圆的周长是它所在圆的周长的一半

答案： C

(2) 如图,点E是圆上一点,圆沿着直尺向右滚动一周后,点E的位置在(D)之间。

A.3cm和4cm
B.4cm和5cm
C.5cm和6cm
D.6cm和7cm

答案： D

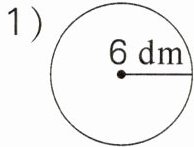
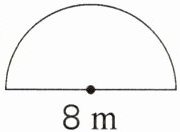
3. 计算下面图形的周长。
(1)

(2)

答案： 3.
(1)2×3.14×6=37.68(dm)
(2)3.14×8÷2+8=20.56(m)

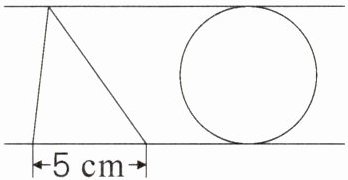
4. 如图,圆的周长是18.84cm,三角形的面积是多少平方厘米？

答案： 18.84÷3.14×5÷2=15(cm²)

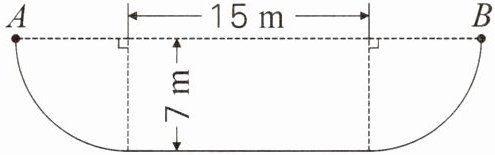
5. 下图是一个U型滑雪场地,李乐从A点沿着图中实线滑行到B点,滑过的路线可以近似看作两个半径相同的$\frac{1}{4}$圆周和一条长15m的线段的组合。李乐滑过的路程是多少米？

答案： 2×3.14×7÷2+15=36.98(m)

6. (说理题)才才和元元用卫生纸纸芯做笔筒,他们分别把4个纸芯用彩绳捆绑固定,两人的捆绑方式如下图(打结处长度和纸芯厚度忽略不计)。已知纸芯的直径约为3cm,这两种捆法所用彩绳的长度相等吗？请说明你的理由。

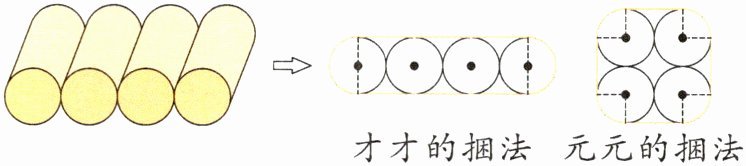
答案： 这两种捆法所用彩绳的长度不相等,理由如下:
才才:3.14×3+3×6=27.42(cm)
元元:3.14×3+3×4=21.42(cm)
【解析】先求出两种捆法分别所用彩绳的长度,再进行比较。观察才才的捆法,彩绳的长度包含两部分,两段曲线部分可以合成一个整圆,直线部分一共是6条直径的长度,所以所用彩绳的长度=一个圆的周长+6条直径的长度。观察元元的捆法,四段曲线部分也可以合成一个整圆,直线部分一共是4条直径的长度,所以所用彩绳的长度=一个圆的周长+4条直径的长度。