第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
3. 如图,在方格纸中,点 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $,$ G $ 均在格点上,则 $ \triangle ABC $ 的重心是(
$ A $. 点 $ G $ $ B $. 点 $ D $ $ C $. 点 $ E $ $ D $. 点 $ F $

B
)$ A $. 点 $ G $ $ B $. 点 $ D $ $ C $. 点 $ E $ $ D $. 点 $ F $

答案:
B
4. 如图,在 $ \triangle ABC $ 中,如果过点 $ B $ 作 $ PB \perp BC $ 交边 $ AC $ 于点 $ P $,过点 $ C $ 作 $ CQ \perp AB $ 交 $ AB $ 的延长线于点 $ Q $,那么图中线段

CQ
是 $ \triangle ABC $ 的一条高.
答案:
$CQ$
5. 如图,$ AE $ 是 $ \triangle ABC $ 的中线,点 $ D $ 在边 $ AB $ 上,$ AD = 2 BD $,$ CD $ 与 $ AE $ 交于点 $ F $,设 $ \triangle ADF $ 的面积为 $ S _ { 1 } $,$ \triangle CEF $ 的面积为 $ S _ { 2 } $,若 $ S _ { \triangle ABC } = 9 $,则 $ S _ { 1 } - S _ { 2 } = $(
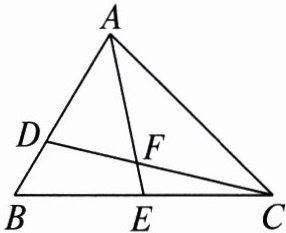
$ A $. $ \frac { 1 } { 2 } $ $ B $. $ 1 $
$ C $. $ \frac { 3 } { 2 } $ $ D $. $ 2 $
C
)
$ A $. $ \frac { 1 } { 2 } $ $ B $. $ 1 $
$ C $. $ \frac { 3 } { 2 } $ $ D $. $ 2 $
答案:
C
6. 如图,在 $ \triangle ABC $ 中,$ \angle 1 = \angle 2 $,$ G $ 是 $ AD $ 的中点,延长 $ BG $ 交 $ AC $ 于点 $ E $,$ F $ 为 $ AB $ 上一点,$ CF \perp AD $ 交 $ AD $ 于点 $ H $.①$ AD $ 是 $ \triangle ABE $ 的角平分线;②$ BE $ 是 $ \triangle ABD $ 的边 $ AD $ 上的中线;③$ CH $ 为 $ \triangle ACD $ 的边 $ AD $ 上的高;④$ AH $ 是 $ \triangle ACF $ 的角平分线和高线. 上述说法正确的有

③④
.(填序号)
答案:
③④
7. 请仅用无刻度的直尺完成下列画图(不写画法,保留画图痕迹).
(1)如图 1,在 $ \triangle ABC $ 中,$ E $,$ F $ 分别为 $ AB $,$ BC $ 的中点,请在图 1 中画出 $ AC $ 的中点 $ M $;
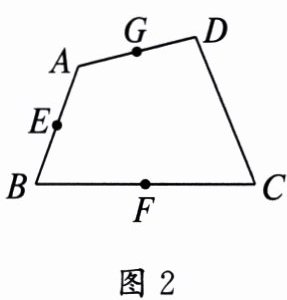
(2)如图 2,在四边形 $ ABCD $ 中,$ E $,$ F $,$ G $ 分别为 $ AB $,$ BC $,$ AD $ 的中点,请在图 2 中画出 $ CD $ 的中点 $ N $.

(1)如图 1,在 $ \triangle ABC $ 中,$ E $,$ F $ 分别为 $ AB $,$ BC $ 的中点,请在图 1 中画出 $ AC $ 的中点 $ M $;
(2)如图 2,在四边形 $ ABCD $ 中,$ E $,$ F $,$ G $ 分别为 $ AB $,$ BC $,$ AD $ 的中点,请在图 2 中画出 $ CD $ 的中点 $ N $.


答案:
(1) 图1中,连接EF,过点F作直线平行于AB,交AC于点M,点M即为AC的中点。(画图痕迹:连接EF,过F作平行AB的直线交AC于M)
(2) 图2中,连接EG,过点F作直线平行于EG,交CD于点N,点N即为CD的中点。(画图痕迹:连接EG,过F作平行EG的直线交CD于N)
(1) 图1中,连接EF,过点F作直线平行于AB,交AC于点M,点M即为AC的中点。(画图痕迹:连接EF,过F作平行AB的直线交AC于M)
(2) 图2中,连接EG,过点F作直线平行于EG,交CD于点N,点N即为CD的中点。(画图痕迹:连接EG,过F作平行EG的直线交CD于N)
8. 如图,在 $ \triangle ABC $ 中,$ AD \perp BC $,$ CE \perp AB $,垂足分别为点 $ D $ 和点 $ E $,$ AD $ 与 $ CE $ 交于点 $ O $,连接 $ BO $ 并延长交 $ AC $ 于点 $ F $,若 $ AB = 5 $,$ BC = 4 $,$ AC = 6 $,则 $ CE : AD : BF $ 的值为

12:15:10
.
答案:
12:15:10
查看更多完整答案,请扫码查看


