第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 如图,若AD= AC,∠BAD= ∠CAE,则添加一个条件不能证明△ABC≌△AED的是(
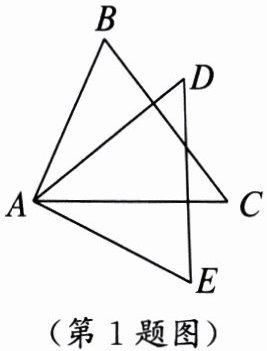
A.AB= AE
B.∠B= ∠E
C.∠C= ∠D
D.BC= DE
D
)
A.AB= AE
B.∠B= ∠E
C.∠C= ∠D
D.BC= DE
答案:
D
2. (2024·黑龙江牡丹江中考)如图,在△ABC中,D是AB上一点,CF//AB,D,E,F三点共线,请添加一个条件
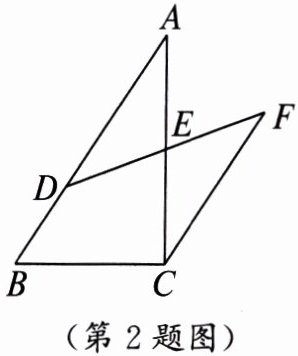
AD=CF(或∠A=∠ECF或DE=FE等,答案不唯一)
,使得AE= CE。
答案:
AD=CF(或∠A=∠ECF或DE=FE等,答案不唯一)
3. 如图,在△ABC中,AB= AC,AB>BC,点D在边BC上,CD= 2BD,点E,F在线段AD上,∠1= ∠2= ∠BAC,若△ABC的面积为18,则△ACF与△BDE的面积之和是(

A.6
B.8
C.9
D.12
A
)
A.6
B.8
C.9
D.12
答案:
A
4. 如图,AB//CD,AE//CF,BF= DE。求证AB= CD。
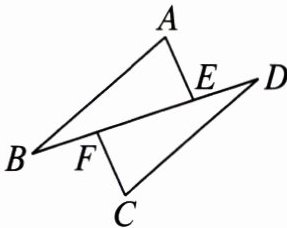

答案:
证明:
∵$AB// CD$,
根据两直线平行,内错角相等,
∴$\angle B = \angle D$。
∵$AE// CF$,
∴$\angle AEF = \angle CFB$。
又因为$\angle AEB + \angle AEF = 180^{\circ}$,$\angle CFB + \angle CFD = 180^{\circ}$。
∴$\angle AEB = \angle CFD$。
∵$BF = DE$,
∴$BF + EF = DE + EF$,
即$BE = DF$。
在$\triangle ABE$和$\triangle CDF$中,
$\begin{cases} \angle B = \angle D,\\BE = DF, \\ \angle AEB = \angle CFD.\end{cases}$
根据$ASA$(角边角)判定定理。
∴$\triangle ABE ≌ \triangle CDF$。
∴$AB = CD$。
∵$AB// CD$,
根据两直线平行,内错角相等,
∴$\angle B = \angle D$。
∵$AE// CF$,
∴$\angle AEF = \angle CFB$。
又因为$\angle AEB + \angle AEF = 180^{\circ}$,$\angle CFB + \angle CFD = 180^{\circ}$。
∴$\angle AEB = \angle CFD$。
∵$BF = DE$,
∴$BF + EF = DE + EF$,
即$BE = DF$。
在$\triangle ABE$和$\triangle CDF$中,
$\begin{cases} \angle B = \angle D,\\BE = DF, \\ \angle AEB = \angle CFD.\end{cases}$
根据$ASA$(角边角)判定定理。
∴$\triangle ABE ≌ \triangle CDF$。
∴$AB = CD$。
5. 如图1,已知△ABC中,∠BAC= 90°,AB= AC,AE是过点A的一条直线,且点B和点C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E。
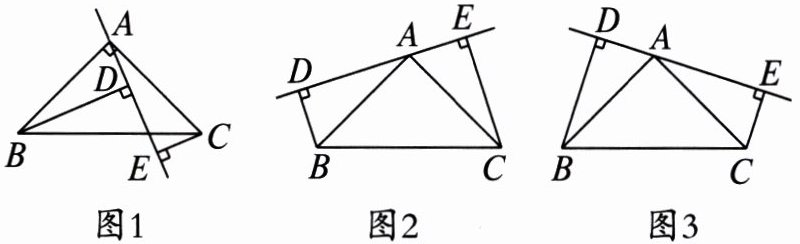
(1)求证:BD= DE+CE。
(2)如图2,若直线AE绕点A旋转到该位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何?请予以证明。
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需说明理由。

(1)求证:BD= DE+CE。
(2)如图2,若直线AE绕点A旋转到该位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何?请予以证明。
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需说明理由。
答案:
(1)证明:
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠ABD+∠BAD=90°,
∴∠ABD=∠CAE(同角的余角相等).
在△ABD和△CAE中,
$\left\{\begin{array}{l}∠ADB=∠CEA\\∠ABD=∠CAE\\AB=AC\end{array}\right.$,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE=AD+DE,
∴BD=CE+DE,即BD=DE+CE.
(2)BD=CE-DE.
证明:
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠ACE+∠CAE=90°,
∴∠BAD=∠ACE(同角的余角相等).
在△ABD和△CAE中,
$\left\{\begin{array}{l}∠ADB=∠CEA\\∠BAD=∠ACE\\AB=AC\end{array}\right.$,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵DE=AD-AE,
∴DE=CE-BD,即BD=CE-DE.
(3)BD=DE-CE.
(1)证明:
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠ABD+∠BAD=90°,
∴∠ABD=∠CAE(同角的余角相等).
在△ABD和△CAE中,
$\left\{\begin{array}{l}∠ADB=∠CEA\\∠ABD=∠CAE\\AB=AC\end{array}\right.$,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE=AD+DE,
∴BD=CE+DE,即BD=DE+CE.
(2)BD=CE-DE.
证明:
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠ACE+∠CAE=90°,
∴∠BAD=∠ACE(同角的余角相等).
在△ABD和△CAE中,
$\left\{\begin{array}{l}∠ADB=∠CEA\\∠BAD=∠ACE\\AB=AC\end{array}\right.$,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵DE=AD-AE,
∴DE=CE-BD,即BD=CE-DE.
(3)BD=DE-CE.
查看更多完整答案,请扫码查看


