第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
2. 一副三角尺摆放方式如图所示,则∠BAC的度数为(
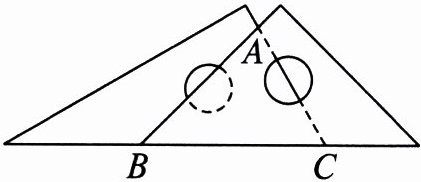
A.75°
B.60°
C.105°
D.120°
C
)
A.75°
B.60°
C.105°
D.120°
答案:
C
3. 在△ABC中,∠B= 2∠A,∠C= ∠A+20°,求△ABC各个内角的度数。
答案:
设$\angle A = x$,则根据题意有:
$\angle B = 2x$,
$\angle C = x + 20^{\circ}$,
根据三角形内角和定理,三角形的三个内角之和为$180 ^{\circ}$,即:
$\angle A + \angle B + \angle C = 180 ^{\circ}$,
代入之前设定的角度表达式,得:
$x + 2x + x + 20 ^{\circ} = 180 ^{\circ}$,
合并同类项,得:
$4x + 20 ^{\circ} = 180 ^{\circ}$,
移项并化简,得:
$4x = 160 ^{\circ}$,
解得:
$x = 40 ^{\circ}$,
将$x = 40 ^{\circ}$代入之前设定的角度表达式中,得:
$\angle A = 40 ^{\circ}$,
$\angle B = 2 × 40 ^{\circ} = 80 ^{\circ}$,
$\angle C = 40 ^{\circ} + 20 ^{\circ} = 60 ^{\circ}$。
所以,$\bigtriangleup ABC$的各个内角分别为:
$\angle A = 40 ^{\circ}$,
$\angle B = 80 ^{\circ}$,
$\angle C = 60 ^{\circ}$。
$\angle B = 2x$,
$\angle C = x + 20^{\circ}$,
根据三角形内角和定理,三角形的三个内角之和为$180 ^{\circ}$,即:
$\angle A + \angle B + \angle C = 180 ^{\circ}$,
代入之前设定的角度表达式,得:
$x + 2x + x + 20 ^{\circ} = 180 ^{\circ}$,
合并同类项,得:
$4x + 20 ^{\circ} = 180 ^{\circ}$,
移项并化简,得:
$4x = 160 ^{\circ}$,
解得:
$x = 40 ^{\circ}$,
将$x = 40 ^{\circ}$代入之前设定的角度表达式中,得:
$\angle A = 40 ^{\circ}$,
$\angle B = 2 × 40 ^{\circ} = 80 ^{\circ}$,
$\angle C = 40 ^{\circ} + 20 ^{\circ} = 60 ^{\circ}$。
所以,$\bigtriangleup ABC$的各个内角分别为:
$\angle A = 40 ^{\circ}$,
$\angle B = 80 ^{\circ}$,
$\angle C = 60 ^{\circ}$。
4. 如图,∠A+∠B+∠C+∠D+∠E的度数为(
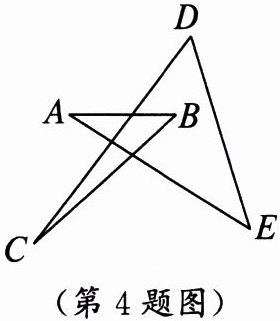
A.180°
B.210°
C.270°
D.360°
A
)
A.180°
B.210°
C.270°
D.360°
答案:
A
5. 如图,在△ABC中,BE,CF是角平分线,BE,CF相交于点D,连接AD,∠ABC= 50°,∠ACB= 70°,则∠ADE为
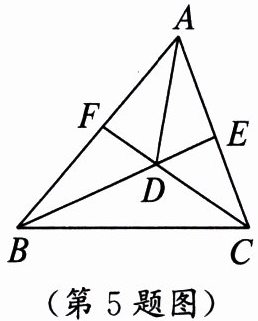
55°
。
答案:
55°
6. (1)如图1,AB和CD交于点O,求证:∠A+∠C= ∠B+∠D;
(2)如图2,AE,CE分别平分∠BAD,∠BCD,运用(1)的结论求证:∠B+∠D= 2∠E。
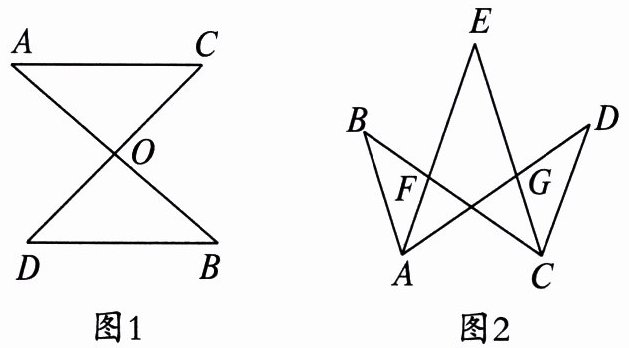
(2)如图2,AE,CE分别平分∠BAD,∠BCD,运用(1)的结论求证:∠B+∠D= 2∠E。

答案:
(1)证明:在△AOC中,∠A+∠C+∠AOC=180°;在△BOD中,∠B+∠D+∠BOD=180°。
∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD。
∴∠A+∠C+∠AOC=∠B+∠D+∠BOD,
∴∠A+∠C=∠B+∠D。
(2)证明:设AE平分∠BAD,CE平分∠BCD,
∴∠BAE=∠EAD=∠BAD/2,∠BCE=∠ECD=∠BCD/2。
设AE与CD交于点F,CE与AB交于点G。
在交点F处,由
(1)得∠D+∠EAD=∠E+∠ECD,即∠D+∠BAD/2=∠E+∠BCD/2 ①;
在交点G处,由
(1)得∠B+∠BCE=∠E+∠BAE,即∠B+∠BCD/2=∠E+∠BAD/2 ②。
①+②得:∠B+∠D+(∠BAD+∠BCD)/2=2∠E+(∠BAD+∠BCD)/2,
∴∠B+∠D=2∠E。
(1)证明:在△AOC中,∠A+∠C+∠AOC=180°;在△BOD中,∠B+∠D+∠BOD=180°。
∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD。
∴∠A+∠C+∠AOC=∠B+∠D+∠BOD,
∴∠A+∠C=∠B+∠D。
(2)证明:设AE平分∠BAD,CE平分∠BCD,
∴∠BAE=∠EAD=∠BAD/2,∠BCE=∠ECD=∠BCD/2。
设AE与CD交于点F,CE与AB交于点G。
在交点F处,由
(1)得∠D+∠EAD=∠E+∠ECD,即∠D+∠BAD/2=∠E+∠BCD/2 ①;
在交点G处,由
(1)得∠B+∠BCE=∠E+∠BAE,即∠B+∠BCD/2=∠E+∠BAD/2 ②。
①+②得:∠B+∠D+(∠BAD+∠BCD)/2=2∠E+(∠BAD+∠BCD)/2,
∴∠B+∠D=2∠E。
查看更多完整答案,请扫码查看


