《2025年阳光课堂金牌练习册八年级数学上册人教版福建专版》

【典型例题】如图,已知点$D$,$E$,$F分别是\triangle ABC$的三边上的点,$CE = BF$,且$\triangle DCE的面积与\triangle DBF$的面积相等,连接$DE$,$DF$,$AD$. 求证：$AD平分\angle BAC$.

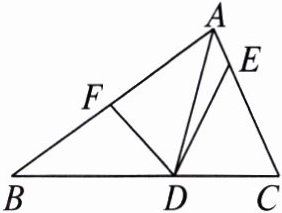
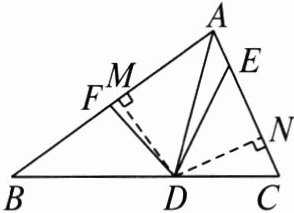
【证明】如图,过$D作DM \perp AB于M$,$DN \perp AC于N$. 因为$\triangle DCE的面积与\triangle DBF$的面积相等,所以$\frac{BF \cdot DM}{2} = \frac{CE \cdot DN}{2}$. 因为$CE = BF$,所以$DM = DN$. 又因为$DM \perp AB$,$DN \perp AC$,所以点$D在\angle BAC$的平分线上,所以$AD平分\angle BAC$.

规律方法 证明角的平分线的步骤：
(1)找出与角的两边都垂直的线段的交点；(2)证明过这一点且到该角的两边的两条垂线段相等；(3)根据角的内部到角两边距离相等的点在角平分线上,证明角平分线.

答案： 【证明】
过点 $D$ 作 $DM \perp AB$ 于 $M$，$DN \perp AC$ 于 $N$。
$\triangle DCE$ 的面积 $= \frac{1}{2} × CE × DN$，
$\triangle DBF$ 的面积 $= \frac{1}{2} × BF × DM$。
因为 $\triangle DCE$ 的面积与 $\triangle DBF$ 的面积相等，且 $CE = BF$，
所以 $\frac{1}{2} × CE × DN = \frac{1}{2} × BF × DM$，
即 $DN = DM$。
因为 $DM \perp AB$，$DN \perp AC$，且 $DM = DN$，
所以点 $D$ 在 $\angle BAC$ 的平分线上。
因此，$AD$ 平分 $\angle BAC$。

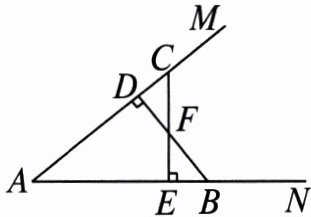
1. 如图,点$B$,$C分别在\angle MAN$的两边上,$BD \perp AM于点D$,$CE \perp AN于点E$,$BD$,$CE相交于点F$,且$BF = CF$. 求证：点$F在\angle MAN$的平分线上.

答案： 证明：
∵$BD\perp AM$，$CE\perp AN$，
∴$\angle FDC=\angle FEB = 90^{\circ}$。
在$\triangle FDC$和$\triangle FEB$中，
$\begin{cases}\angle FDC=\angle FEB\\\angle DFC=\angle EFB\\CF = BF\end{cases}$，
∴$\triangle FDC\cong\triangle FEB(AAS)$，
∴$FD = FE$。
∵$FD\perp AM$，$FE\perp AN$，
∴点$F$在$\angle MAN$的平分线上。

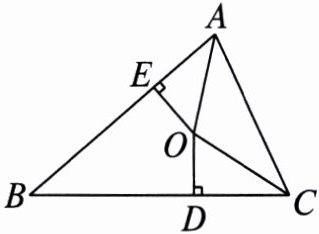
2. 如图,已知$AO平分\angle BAC$,$OD \perp BC$,$OE \perp AB$,垂足分别为$D$,$E$,且$OD = OE$. 求证：$CO平分\angle ACB$.

答案： 过点$O$作$OF\perp AC$，垂足为$F$。
因为$AO$平分$\angle BAC$，$OE\perp AB$，$OF\perp AC$，
根据角平分线的性质：角平分线上的点到角两边的距离相等，
所以$OE = OF$。
已知$OD = OE$，所以$OD = OF$。
因为$OD\perp BC$，$OF\perp AC$，
根据到角两边距离相等的点在角的平分线上，
所以$CO$平分$\angle ACB$。

1. 一块三角形的草坪如图所示,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(C)

A.$\triangle ABC$三条中线的交点
B.$\triangle ABC$三条高所在直线的交点
C.$\triangle ABC$三条角平分线的交点
D.以上都不对

答案： C