第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
2.(2024·云南中考)已知 AF 是等腰三角形 ABC 底边 BC 上的高.若点 F 到直线 AB 的距离为 3,则点 F 到直线 AC 的距离为(
A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
C
)A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
答案:
C
1. 如图 1,已知∠AOB,只用直尺和圆规,如何判断∠AOB 是否为直角?如图 2,小意在 OA,OB 上分别取 C,D,以点 C 为圆心,CD 的长为半径画弧,交 OB 的反向延长线于点 E.若测量得 OE = OD,则∠AOB = 90°.小意判断的依据是(
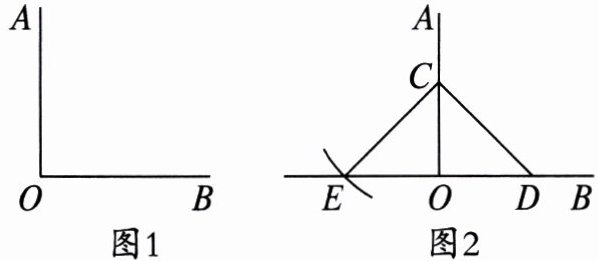
A.等边对等角
B.线段垂直平分线上的点到线段两端点的距离相等
C.垂线段最短
D.等腰三角形“三线合一”
D
)
A.等边对等角
B.线段垂直平分线上的点到线段两端点的距离相等
C.垂线段最短
D.等腰三角形“三线合一”
答案:
D
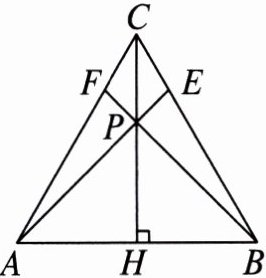
2. 如图,在等腰三角形 ABC 中,CH 是底边上的高,点 P 是线段 CH 上不与端点重合的任意一点,连接 AP 并延长交 BC 于点 E,连接 BP 并延长交 AC 于点 F.求证:
(1)∠CAE = ∠CBF;
(2)AE = BF.
(1)∠CAE = ∠CBF;
(2)AE = BF.

答案:
(1)
∵△ABC是等腰三角形,CH是底边上的高,
∴AC=BC,CH平分∠ACB(三线合一),即∠ACP=∠BCP。
在△ACP和△BCP中,
$\left\{\begin{array}{l} AC=BC \\ ∠ACP=∠BCP \\ CP=CP \end{array}\right.$
∴△ACP≌△BCP(SAS),
∴∠CAP=∠CBP,即∠CAE=∠CBF。
(2)在△ACE和△BCF中,
$\left\{\begin{array}{l} ∠CAE=∠CBF \\ AC=BC \\ ∠ACE=∠BCF \end{array}\right.$
∴△ACE≌△BCF(ASA),
∴AE=BF。
∵△ABC是等腰三角形,CH是底边上的高,
∴AC=BC,CH平分∠ACB(三线合一),即∠ACP=∠BCP。
在△ACP和△BCP中,
$\left\{\begin{array}{l} AC=BC \\ ∠ACP=∠BCP \\ CP=CP \end{array}\right.$
∴△ACP≌△BCP(SAS),
∴∠CAP=∠CBP,即∠CAE=∠CBF。
(2)在△ACE和△BCF中,
$\left\{\begin{array}{l} ∠CAE=∠CBF \\ AC=BC \\ ∠ACE=∠BCF \end{array}\right.$
∴△ACE≌△BCF(ASA),
∴AE=BF。
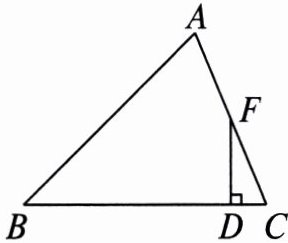
3. 如图,在△ABC 中,AB = BC,DF ⊥ BC 于点 D,交 AC 于点 F.F 是 AC 的中点,求证∠CFD = $\frac{1}{2}$∠B.

答案:
因为 $AB = BC$,$F$ 是 $AC$ 的中点,
根据等腰三角形的性质,等腰三角形底边上的中线、底边上的高线、顶角平角线互相重合,
所以 $BF\bot AC$,$\angle ABF=\angle CBF=\frac{1}{2}\angle B$,
因为 $DF\bot BC$,
所以 $\angle CDF = 90^\circ$,
因为 $BF\bot AC$,
所以 $\angle BFC = 90^\circ$,
所以 $\angle CFD + \angle DCF = 90^\circ$,$\angle CBF + \angle DCF = 90^\circ$,
所以 $\angle CFD = \angle CBF$,
所以 $\angle CFD = \frac{1}{2}\angle B$。
根据等腰三角形的性质,等腰三角形底边上的中线、底边上的高线、顶角平角线互相重合,
所以 $BF\bot AC$,$\angle ABF=\angle CBF=\frac{1}{2}\angle B$,
因为 $DF\bot BC$,
所以 $\angle CDF = 90^\circ$,
因为 $BF\bot AC$,
所以 $\angle BFC = 90^\circ$,
所以 $\angle CFD + \angle DCF = 90^\circ$,$\angle CBF + \angle DCF = 90^\circ$,
所以 $\angle CFD = \angle CBF$,
所以 $\angle CFD = \frac{1}{2}\angle B$。
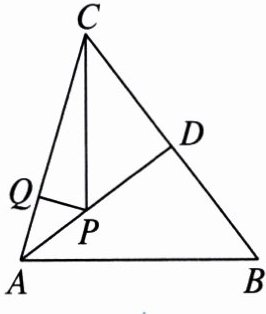
4. 如图,在△ABC 中,AB = AC = 10,BC = 12,AD = 8,AD 是∠BAC 的平分线.若 P,Q 分别是 AD 和 AC 上的动点,则 PC + PQ 的最小值是
48/5
.
答案:
48/5
查看更多完整答案,请扫码查看


