第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
12. (2024·衡阳衡南县期中)已知在 $ \triangle ABC $ 中, $ \sin B = \cos (90^{\circ} - \angle C) = \frac{1}{2} $,那么 $ \triangle ABC $ 是(
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
A
)A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
答案:
A
13. 新考向 新定义问题 定义:一个三角形的一边长是另一边长的 $ 2 $ 倍,这样的三角形叫作“倍长三角形”. 若等腰三角形 $ ABC $ 是“倍长三角形”,则底角的余弦值为(
A.$ \frac{1}{4} $
B.$ \frac{\sqrt{15}}{4} $
C.$ \frac{1}{2} $
D.$ \frac{\sqrt{2}}{2} $
A
)A.$ \frac{1}{4} $
B.$ \frac{\sqrt{15}}{4} $
C.$ \frac{1}{2} $
D.$ \frac{\sqrt{2}}{2} $
答案:
A
14. 在正方形网格中, $ \triangle ABC $ 的位置如图所示,则 $ \cos A $ 的值为
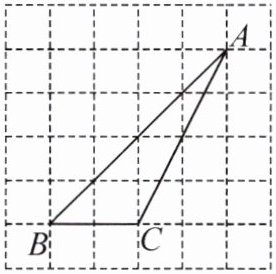
3√10/10
.
答案:
3√10/10
15. 计算: $ 2 \cos 45^{\circ} + (\pi - 3.14)^{0} + | 1 - \sqrt{2} | + (\frac{1}{2})^{-1} $.
答案:
解:原式=2×√2/2+1+√2-1+2=2√2+2.
16. 如图,在 $ Rt\triangle ABC $ 中, $ \angle C = 90^{\circ} $, $ M $ 是直角边 $ AC $ 上一点, $ MN \perp AB $ 于点 $ N $, $ AN = 3 $, $ AM = 4 $,求 $ \cos B $ 的值.
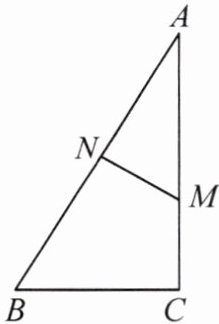

答案:
解:
∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°.又
∵∠A=∠A,
∴△AMN∽△ABC.
∴AC/AB=AN/AM=3/4.设AC=3x,AB=4x,由勾股定理,得BC=√(AB²-AC²)=√7x,在Rt△ABC中,cosB=BC/AB=√7x/4x=√7/4.
∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°.又
∵∠A=∠A,
∴△AMN∽△ABC.
∴AC/AB=AN/AM=3/4.设AC=3x,AB=4x,由勾股定理,得BC=√(AB²-AC²)=√7x,在Rt△ABC中,cosB=BC/AB=√7x/4x=√7/4.
17. 新考向 阅读理解 【数学猜想】
(1)阅读下面的材料,先完成阅读填空,再按要求答题:
$ \sin 30^{\circ} = \frac{1}{2} $, $ \cos 30^{\circ} = \frac{\sqrt{3}}{2} $,则 $ \sin^{2} 30^{\circ} + \cos^{2} 30^{\circ} = $
$ \sin 45^{\circ} = \frac{\sqrt{2}}{2} $, $ \cos 45^{\circ} = \frac{\sqrt{2}}{2} $,则 $ \sin^{2} 45^{\circ} + \cos^{2} 45^{\circ} = $
$ \sin 60^{\circ} = \frac{\sqrt{3}}{2} $, $ \cos 60^{\circ} = \frac{1}{2} $,则 $ \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = $
……
观察上述等式,猜想:对任意锐角 $ A $,都有 $ \sin^{2} A + \cos^{2} A = $
【猜想论证】
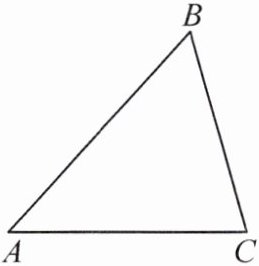
(2)如图,在锐角三角形 $ ABC $ 中,利用三角函数的定义及勾股定理对 $ \angle A $ 证明你的猜想;
【迁移应用】
(3)已知 $ \angle A $ 为锐角 $ (\cos A > 0) $ 且 $ \sin A = \frac{3}{5} $,求 $ \cos A $.
(1)阅读下面的材料,先完成阅读填空,再按要求答题:
$ \sin 30^{\circ} = \frac{1}{2} $, $ \cos 30^{\circ} = \frac{\sqrt{3}}{2} $,则 $ \sin^{2} 30^{\circ} + \cos^{2} 30^{\circ} = $
1
; ①$ \sin 45^{\circ} = \frac{\sqrt{2}}{2} $, $ \cos 45^{\circ} = \frac{\sqrt{2}}{2} $,则 $ \sin^{2} 45^{\circ} + \cos^{2} 45^{\circ} = $
1
; ②$ \sin 60^{\circ} = \frac{\sqrt{3}}{2} $, $ \cos 60^{\circ} = \frac{1}{2} $,则 $ \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = $
1
; ③……
观察上述等式,猜想:对任意锐角 $ A $,都有 $ \sin^{2} A + \cos^{2} A = $
1
;【猜想论证】
(2)如图,在锐角三角形 $ ABC $ 中,利用三角函数的定义及勾股定理对 $ \angle A $ 证明你的猜想;
【迁移应用】
(3)已知 $ \angle A $ 为锐角 $ (\cos A > 0) $ 且 $ \sin A = \frac{3}{5} $,求 $ \cos A $.

答案:
解:
(1)1 1 1 1
(2)证明:过点B作BD⊥AC于点D,则∠ADB=90°.
∵sinA=BD/AB,cosA=AD/AB,
∴sin²A+cos²A=(BD/AB)²+(AD/AB)²=(BD²+AD²)/AB².
∵∠ADB=90°,
∴BD²+AD²=AB².
∴sin²A+cos²A=1.
(3)
∵sinA=3/5,sin²A+cos²A=1,∠A为锐角,
∴cosA=√(1-(3/5)²)=4/5.
(1)1 1 1 1
(2)证明:过点B作BD⊥AC于点D,则∠ADB=90°.
∵sinA=BD/AB,cosA=AD/AB,
∴sin²A+cos²A=(BD/AB)²+(AD/AB)²=(BD²+AD²)/AB².
∵∠ADB=90°,
∴BD²+AD²=AB².
∴sin²A+cos²A=1.
(3)
∵sinA=3/5,sin²A+cos²A=1,∠A为锐角,
∴cosA=√(1-(3/5)²)=4/5.
查看更多完整答案,请扫码查看


