第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,为估算某河的宽度,在河对岸选定一个目标点 $ A $,在近岸取点 $ B $,$ C $,$ D $,使得 $ AB \perp BC $,$ CD \perp BC $,点 $ E $ 在 $ BC $ 上,并且点 $ A $,$ E $,$ D $ 在同一条直线上。若测得 $ BE = 20\ m $,$ CE = 10\ m $,$ CD = 20\ m $,则河的宽度 $ AB $ 等于(
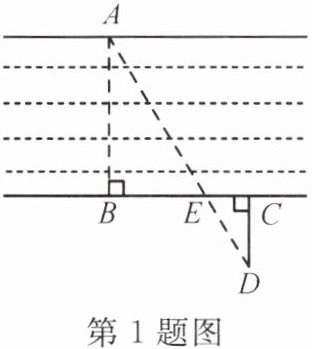
A.$ 60\ m $
B.$ 40\ m $
C.$ 30\ m $
D.$ 20\ m $
B
)
A.$ 60\ m $
B.$ 40\ m $
C.$ 30\ m $
D.$ 20\ m $
答案:
1.B
2. 如图,在河两岸分别有 $ A $,$ B $ 两村,现测得点 $ A $,$ B $,$ D $ 在同一条直线上,点 $ A $,$ C $,$ E $ 在同一条直线上,$ BC // DE $,$ DE = 90 $ 米,$ BC = 70 $ 米,$ BD = 20 $ 米,则 $ A $,$ B $ 两村间的距离为

70
米。
答案:
2.70
3. 如图,这是测量小玻璃管口径的量具 $ ABC $,$ AB $ 的长为 $ 10\ cm $,$ AC $ 被分为 $ 60 $ 等份。如果小玻璃管口 $ DE $ 正好对着量具上 $ 20 $ 等份处,且 $ DE // AB $,那么小玻璃管口径 $ DE $ 是多大?
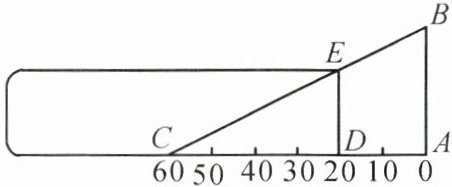

答案:
3.解:
∵DE//AB,
∴△CDE∽△CAB.
∴$\frac{DE}{AB}=\frac{CD}{AC}$.
∴$\frac{DE}{10}=\frac{40}{60}$.
∴DE=$\frac{20}{3}$cm.
答:小玻璃管口径DE是$\frac{20}{3}$cm.
∵DE//AB,
∴△CDE∽△CAB.
∴$\frac{DE}{AB}=\frac{CD}{AC}$.
∴$\frac{DE}{10}=\frac{40}{60}$.
∴DE=$\frac{20}{3}$cm.
答:小玻璃管口径DE是$\frac{20}{3}$cm.
4. 在同一时刻,物体的高度与它在阳光下的影长成正比。在某一时刻,有人测得一根高为 $ 1.8\ m $ 的竹竿的影长为 $ 3\ m $,某一幢高楼的影长为 $ 60\ m $,那么这幢高楼的高度是(
A.$ 18\ m $
B.$ 20\ m $
C.$ 30\ m $
D.$ 36\ m $
D
)A.$ 18\ m $
B.$ 20\ m $
C.$ 30\ m $
D.$ 36\ m $
答案:
4.D
5. (教材 $ P92 $ 练习 $ T1 $ 变式)学校门口的栏杆如图所示,栏杆从水平位置 $ BD $ 绕 $ O $ 点旋转到 $ AC $ 位置。已知 $ AB \perp BD $,$ CD \perp BD $,垂足分别为 $ B $,$ D $,$ AO = 4\ m $,$ AB = 1.6\ m $,$ CO = 1\ m $,则栏杆 $ C $ 端应下降的垂直距离 $ CD $ 为(

A.$ 0.2\ m $
B.$ 0.3\ m $
C.$ 0.4\ m $
D.$ 0.5\ m $
C
)
A.$ 0.2\ m $
B.$ 0.3\ m $
C.$ 0.4\ m $
D.$ 0.5\ m $
答案:
5.C
6. (2023·南充)如图,在数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端。已知小菲的眼睛离地面的高度为 $ 1.6\ m $,同时量得小菲与镜子的水平距离为 $ 2\ m $,镜子与旗杆的水平距离为 $ 10\ m $,则旗杆的高度为(

A.$ 6.4\ m $
B.$ 8\ m $
C.$ 9.6\ m $
D.$ 12.5\ m $
B
)
A.$ 6.4\ m $
B.$ 8\ m $
C.$ 9.6\ m $
D.$ 12.5\ m $
答案:
6.B
7. 如图,为了测量山坡的护坡石坝高,把一根长为 $ 4.5\ m $ 的竹竿 $ AC $ 斜靠在石坝旁,量出竿上 $ AD $ 长为 $ 1\ m $ 时,它离地面的高度 $ DE $ 为 $ 0.6\ m $,则坝高 $ CF $ 为

2.7
$m$。
答案:
7.2.7
8. 新考向 数学文化(2023·潍坊)在《数书九章》中记载了一个测量塔高的问题:如图所示,$ AB $ 表示塔的高度,$ CD $ 表示竹竿顶端到地面的距离,$ EF $ 表示人眼到地面的距离,$ AB $,$ CD $,$ EF $ 在同一平面内,点 $ A $,$ C $,$ E $ 在同一条水平直线上。已知 $ AC = 20 $ 米,$ CE = 10 $ 米,$ CD = 7 $ 米,$ EF = 1.4 $ 米,人从点 $ F $ 远眺塔顶 $ B $,视线恰好经过竹竿的顶端 $ D $。根据以上信息,可求出塔的高度为
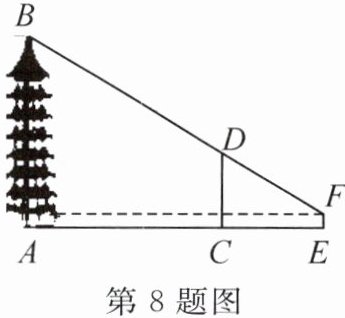
18.2
米。
答案:
8.18.2
查看更多完整答案,请扫码查看


