《2025年名校课堂九年级数学上册湘教版湖南专版》

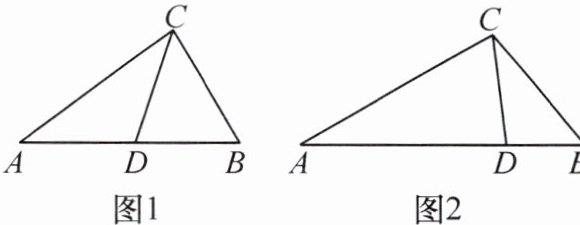
11. 新考向 新定义问题 从三角形 (不是等腰三角形) 一个顶点引出一条射线与对边相交, 顶点与交点之间的线段把这个三角形分割成两个小三角形. 如果分得的两个小三角形中一个为等腰三角形, 另一个与原三角形相似, 我们就把这条线段叫作这个三角形的完美分割线.
(1) 如图 1, 在 $\triangle A B C$ 中, $C D$ 为角平分线, $∠A=40^{\circ},∠B=60^{\circ}$, 求证: $C D$ 是 $\triangle A B C$ 的完美分割线;
(2) 如图 2, 在 $\triangle A B C$ 中, $A C=2, B C=\sqrt{2}$, $C D$ 是 $\triangle A B C$ 的完美分割线, 且 $\triangle A C D$ 是以 $C D$ 为底边的等腰三角形, 求完美分割线 $C D$ 的长.

答案： 11.解:
(1)证明:
∵∠A=40°,∠B=60°,
∴∠ACB=80°.
∴△ABC不是等腰三角形.
∵CD平分∠ACB,
∴∠ACD=∠BCD=$\frac{1}{2}$∠ACB=40°.
∴∠ACD=∠A=40°.
∴△ACD是等腰三角形.
∵∠BCD=∠A=40°,∠CBD=∠ABC,
∴△CBD∽△ABC.
∴CD是△ABC的完美分割线.
(2)设BD=x,由题意,得△CBD∽△ABC,AD=AC=2,则AB=2+x,
∴$\frac{BC}{BA}=\frac{BD}{BC}$.
∴$\frac{\sqrt{2}}{x+2}=\frac{x}{\sqrt{2}}$,解得x=$\sqrt{3}-1$(负值舍去).
∴BD=$\sqrt{3}-1$.
∵△CBD∽△ABC,
∴$\frac{CD}{AC}=\frac{BD}{BC}$.
∴CD=$\frac{AC\cdot BD}{BC}=\frac{2(\sqrt{3}-1)}{\sqrt{2}}=\sqrt{6}-\sqrt{2}$.

1. 如图, 在 $\mathrm{Rt} \triangle A B C$ 中, $A D$ 为斜边 $B C$ 上的高, $∠A B C$ 的平分线 $B E$ 交 $A C$ 于点 $E$, 交 $A D$ 于点 $F$. 求证: $\frac{A B}{B C}=\frac{A F}{C E}$.

答案： 1.证明:
∵在Rt△ABC中,AD为斜边BC上的高,
∴∠C+∠CAD=90°.
∵∠CAD+∠BAD=90°,
∴∠BAD=∠C.
∵∠ABC的平分线BE交AC于点E,
∴∠ABF=∠CBE.
∴△ABF∽△CBE.
∴$\frac{AB}{BC}=\frac{AF}{CE}$.

2. 如图, 在 $\mathrm{Rt} \triangle A B C$ 中有正方形 $D E F G$, 点 $E, F$ 在斜边 $B C$ 上, 点 $D, G$ 分别在边 $A B$, $A C$ 上. 求证: $E F^{2}=B E \cdot F C$.

答案： 2.证明:
∵四边形DEFG为正方形,
∴∠DEB=∠GFC=90°.又
∵∠B与∠C互余,∠FGC与∠C互余,
∴∠B=∠FGC.
∴△BED∽△GFC.
∴$\frac{BE}{DE}=\frac{GF}{FC}$,即DE·GF=BE·CF.又
∵DE=GF=EF,
∴EF²=BE·FC.