第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2024·重庆 B 卷)若两个相似三角形的相似比为 $1:4$,则这两个三角形的面积之比是(
A.$1:2$
B.$1:4$
C.$1:8$
D.$1:16$
D
)A.$1:2$
B.$1:4$
C.$1:8$
D.$1:16$
答案:
D
2. 如图,在$\triangle ABC$中,$DE// BC$,$DE = 2$,$BC = 5$,则$S_{\triangle ADE}:S_{\triangle ABC}$的值是(
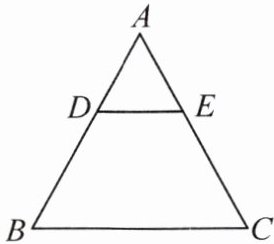
A.$\frac{3}{25}$
B.$\frac{4}{25}$
C.$\frac{2}{5}$
D.$\frac{3}{5}$
B
)
A.$\frac{3}{25}$
B.$\frac{4}{25}$
C.$\frac{2}{5}$
D.$\frac{3}{5}$
答案:
B
3. (2024·邵阳洞口县期中)已知$\triangle ABC\backsim\triangle DEF$,$AB = 12\mathrm{cm}$,$DE = 8\mathrm{cm}$,$\triangle ABC$的面积为$81\mathrm{cm}^2$,则$\triangle DEF$的面积为
36
$\mathrm{cm}^2$.
答案:
36
4. 如图,点$D$,$E$分别在$\triangle ABC$的边$AC$,$AB$上,$\triangle ADE\backsim\triangle ABC$,$M$,$N$分别是$DE$,$BC$的中点.若$\frac{AM}{AN}=\frac{1}{2}$,则$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=$

$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
5. 如图,四边形$ABCD$为平行四边形,$E$,$F$为$CD$边的两个三等分点,连接$AF$,$BE$交于点$G$,则$S_{\triangle EFG}:S_{\triangle ABG}=$
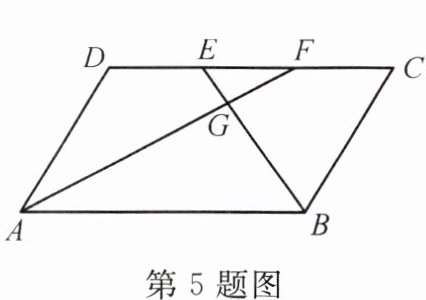
$\frac{1}{9}$
.
答案:
$\frac{1}{9}$
6. (2023·岳阳汨罗市期中)如图,在$\triangle ABC$和$\triangle DEC$中,$\angle A=\angle D$,$\angle BCE=\angle ACD$.
(1)求证:$\triangle ABC\backsim\triangle DEC$;
(2)若$S_{\triangle ABC}:S_{\triangle DEC}=4:9$,$BC = 6$,求$EC$的长.
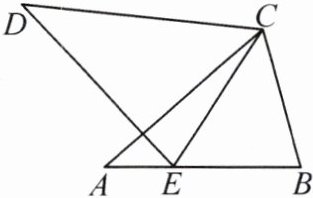
(1)求证:$\triangle ABC\backsim\triangle DEC$;
(2)若$S_{\triangle ABC}:S_{\triangle DEC}=4:9$,$BC = 6$,求$EC$的长.

答案:
(1)证明:$\because \angle BCE=\angle ACD$,$\therefore \angle BCE+\angle ACE=\angle ACD+\angle ACE$,即$\angle ACB=\angle DCE$.又$\because \angle A=\angle D$,$\therefore \triangle ABC\backsim \triangle DEC$.
(2)$\because \triangle ABC\backsim \triangle DEC$,$\therefore \frac{S_{\triangle ABC}}{S_{\triangle DEC}}=\left(\frac{BC}{EC}\right)^2=\frac{4}{9}$.$\therefore \frac{BC}{EC}=\frac{2}{3}$,即$\frac{6}{EC}=\frac{2}{3}$.$\therefore EC=9$.
(1)证明:$\because \angle BCE=\angle ACD$,$\therefore \angle BCE+\angle ACE=\angle ACD+\angle ACE$,即$\angle ACB=\angle DCE$.又$\because \angle A=\angle D$,$\therefore \triangle ABC\backsim \triangle DEC$.
(2)$\because \triangle ABC\backsim \triangle DEC$,$\therefore \frac{S_{\triangle ABC}}{S_{\triangle DEC}}=\left(\frac{BC}{EC}\right)^2=\frac{4}{9}$.$\therefore \frac{BC}{EC}=\frac{2}{3}$,即$\frac{6}{EC}=\frac{2}{3}$.$\therefore EC=9$.
7. 已知$\triangle FHB\backsim\triangle EAD$,它们的周长分别为$30$和$15$,且$FH = 6$,则$EA$的长为(
A.$3$
B.$2$
C.$4$
D.$5$
A
)A.$3$
B.$2$
C.$4$
D.$5$
答案:
A
8. 若$\triangle ABC\backsim\triangle DEF$,且$S_{\triangle ABC}:S_{\triangle DEF}=3:4$,则$\triangle ABC$与$\triangle DEF$的周长比为(
A.$3:4$
B.$4:3$
C.$\sqrt{3}:2$
D.$2:\sqrt{3}$
C
)A.$3:4$
B.$4:3$
C.$\sqrt{3}:2$
D.$2:\sqrt{3}$
答案:
C
9. (2024·云南)如图,$AB$与$CD$相交于点$O$,且$AC// BD$.若$\frac{OA + OC + AC}{OB + OD + BD}=\frac{1}{2}$,则$\frac{AC}{BD}=$

$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
10. 如图,在$\mathrm{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$.
(1)在$AB$上求作一点$D$,使$\triangle ABC\backsim\triangle CBD$(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求$\triangle ACD$的周长.
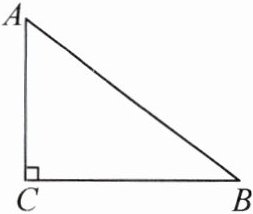
(1)在$AB$上求作一点$D$,使$\triangle ABC\backsim\triangle CBD$(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求$\triangle ACD$的周长.

答案:
(1)图略.
(2)$\because \angle ACB=90°$,$AC=3$,$BC=4$,$\therefore AB=\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$.$\therefore \triangle ABC$的周长为$3+4+5=12$.$\because \angle A=\angle A$,$\angle ACB=\angle ADC=90°$,$\therefore \triangle ABC\backsim \triangle ACD$.$\therefore \frac{\triangle ABC的周长}{\triangle ACD的周长}=\frac{AB}{AC}=\frac{5}{3}$.$\therefore \triangle ACD$的周长为$\frac{3}{5}× 12=\frac{36}{5}$.
(1)图略.
(2)$\because \angle ACB=90°$,$AC=3$,$BC=4$,$\therefore AB=\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$.$\therefore \triangle ABC$的周长为$3+4+5=12$.$\because \angle A=\angle A$,$\angle ACB=\angle ADC=90°$,$\therefore \triangle ABC\backsim \triangle ACD$.$\therefore \frac{\triangle ABC的周长}{\triangle ACD的周长}=\frac{AB}{AC}=\frac{5}{3}$.$\therefore \triangle ACD$的周长为$\frac{3}{5}× 12=\frac{36}{5}$.
查看更多完整答案,请扫码查看


