第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7. (2024·扬州宝应模拟)“塔吊”是修建高层建筑常见的起重设备,又名“塔式起重机”。某“塔吊”以恒定功率 24 kW,将质量为 2 t 的重物从静止开始竖直向上提升 45 s,全程的 v - t 关系如图所示。g 取 10 N/kg,忽略空气阻力和摩擦。求:
(1)$t= 30s$时重物所受的拉力。
(2) 整个过程中重物的最大速度。
(3) 若重物上升的总高度为 60 m,则最后 12 s 拉力所做的功为多大?

(1)$t= 30s$时重物所受的拉力。
(2) 整个过程中重物的最大速度。
(3) 若重物上升的总高度为 60 m,则最后 12 s 拉力所做的功为多大?

答案:
(1)$2×10^{4}\ \text{N}$ (2)$1.2\ \text{m/s}$ (3)$1.2×10^{5}\ \text{J}$ 提示:(1)15~45 s内,重物匀速运动,$F=G=mg=2×10^{3}\ \text{kg}×10\ \text{N/kg}=2×10^{4}\ \text{N}$。(2)$P=24\ \text{kW}=2.4×10^{4}\ \text{W}$,由$P=\frac{W}{t}=\frac{Fs}{t}=Fv$得$v_{绳}=\frac{P}{F}=\frac{2.4×10^{4}\ \text{W}}{2×10^{4}\ \text{N}}=1.2\ \text{m/s}$。(3)忽略空气阻力和摩擦,$W_{G}=Gh=2×10^{4}\ \text{N}×60\ \text{m}=1.2×10^{6}\ \text{J}$,前45 s拉力做功$W_{1}=Pt_{1}=2.4×10^{4}\ \text{W}×45\ \text{s}=1.08×10^{6}\ \text{J}$,最后12 s拉力做功$W_{2}=W_{G}-W_{1}=1.2×10^{6}\ \text{J}-1.08×10^{6}\ \text{J}=1.2×10^{5}\ \text{J}$。
8. (2024·镇江丹徒模拟)如图所示,湖水中有两艘小船,绳子的一端拴在甲船上,乙船上固定着滑轮,绳子绕过滑轮,站在甲船上的人用 100 N 的力拉绳子的自由端。如果在 20 s 内甲船向右匀速移动了 10 m,同时乙船向左匀速移动了 4 m,则下列说法正确的是 (
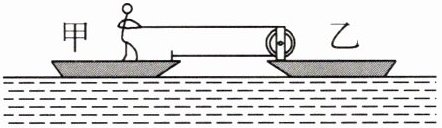
A.人对绳子的拉力做功的功率是 100 W
B.绳子自由端移动的距离为 20 m
C.绳子自由端移动的速度为 1.4 m/s
D.甲船受到的拉力为 100 N,乙船受到的拉力为 100 N
C
)
A.人对绳子的拉力做功的功率是 100 W
B.绳子自由端移动的距离为 20 m
C.绳子自由端移动的速度为 1.4 m/s
D.甲船受到的拉力为 100 N,乙船受到的拉力为 100 N
答案:
C 提示:甲船和乙船都有两段绳子承担拉力,故两船受到的拉力均为200 N;以甲为参照物,乙向左移动14 m,绳子自由端移动的距离$s=14\ \text{m}×2=28\ \text{m}$,人拉绳子的功率$P=\frac{W}{t}=\frac{Fs}{t}=\frac{100\ \text{N}×28\ \text{m}}{20\ \text{s}}=140\ \text{W}$,绳子自由端的速度$v=\frac{s}{t}=\frac{28\ \text{m}}{20\ \text{s}}=1.4\ \text{m/s}$。
9. 汽车在平直公路上以速度$v_{0}$匀速行驶,发动机功率为$P_{0}$,牵引力为$F_{0}$。$t_{1}$时刻开始,司机减小了油门,汽车以另一恒定功率 P 行驶,到$t_{2}$时刻,汽车又开始做匀速直线运动,速度为 v。已知运动过程中汽车所受阻力 f 恒定不变,汽车牵引力 F 随时间 t 变化的图像如图所示,则 (

A.$F_{0}= 2f$
B.$t_{1}\sim t_{2}$时间内,汽车做加速运动
C.$v= 2v_{0}$
D.$t_{2}$时刻之后,$P= \frac {P_{0}}{2}$
D
)
A.$F_{0}= 2f$
B.$t_{1}\sim t_{2}$时间内,汽车做加速运动
C.$v= 2v_{0}$
D.$t_{2}$时刻之后,$P= \frac {P_{0}}{2}$
答案:
D 提示:汽车做匀速直线运动时,牵引力与阻力平衡,即$F_{0}=f$。$t_{1}\sim t_{2}$时间内,汽车受到的牵引力增大,功率不变,由$P=Fv$知汽车做减速运动。在$t_{1}$时刻前,$P_{0}=F_{0}v_{0}$,在$t_{1}$时刻,汽车的速度不变,牵引力由$F_{0}$突然减小为$\frac{1}{2}F_{0}$,$P=\frac{1}{2}F_{0}v_{0}$,得$P=\frac{1}{2}P_{0}$。到$t_{2}$时刻,速度为v,牵引力为$F_{0}$,$v=\frac{P}{F_{0}}=\frac{\frac{1}{2}P_{0}}{F_{0}}=\frac{\frac{1}{2}F_{0}v_{0}}{F_{0}}=\frac{1}{2}v_{0}$。
10. 一辆小轿车以 15 m/s 的速度在水平公路上匀速行驶,受到的阻力是 1 200 N,小轿车沿水平路面匀速行驶 300 m 后驶上一个斜坡。设行驶过程中小轿车的功率始终保持不变,行驶过程中小轿车的功率是
18
kW;要使小轿车上坡时的牵引力增大为水平路面时的 1.5 倍,其行驶速度应为10
m/s。
答案:
18 10 提示:小轿车做匀速直线运动时,$F=F_{阻}=1200\ \text{N}$,$P=\frac{W}{t}=\frac{Fs}{t}=Fv=1200\ \text{N}×15\ \text{m/s}=1.8×10^{4}\ \text{W}=18\ \text{kW}$;$P_{1}=P_{2}$,有$F_{1}v_{1}=F_{2}v_{2}$,$v_{2}=\frac{F_{1}v_{1}}{F_{2}}=\frac{v_{1}}{1.5}=\frac{15\ \text{m/s}}{1.5}=10\ \text{m/s}$。
查看更多完整答案,请扫码查看


