《2025年假期伙伴暑假大连理工大学出版社五年级数学北师大版》

1. 计算。
$\frac{5}{24}÷\frac{5}{12}$
$\frac{15}{16}÷\frac{3}{8}$
$\frac{8}{9}÷\frac{5}{12}$

答案： 【解析】：根据分数除法的运算法则，除以一个分数等于乘以这个分数的倒数。
对于$\frac{5}{24}÷\frac{5}{12}$，$\frac{5}{24}÷\frac{5}{12}=\frac{5}{24}×\frac{12}{5}$，分子分母约分后，$\frac{5×12}{24×5}=\frac{1}{2}$。
对于$\frac{15}{16}÷\frac{3}{8}$，$\frac{15}{16}÷\frac{3}{8}=\frac{15}{16}×\frac{8}{3}$，分子分母约分后，$\frac{15×8}{16×3}=\frac{5}{2}$。
对于$\frac{8}{9}÷\frac{5}{12}$，$\frac{8}{9}÷\frac{5}{12}=\frac{8}{9}×\frac{12}{5}$，分子分母约分后，$\frac{8×12}{9×5}=\frac{32}{15}$。
【答案】：$\frac{1}{2}$；$\frac{5}{2}$；$\frac{32}{15}$

2. 解方程。
$\frac{4}{5}x=20$，解得$x =$25
$\frac{5}{12}x+4=16$，解得$x =$28.8
$\frac{2}{3}x+\frac{1}{5}x=26$，解得$x =$30

答案： 【解析】：
1. 对于方程$\frac{4}{5}x = 20$：
根据等式的性质，等式两边同时除以一个非零数，等式仍然成立。在方程两边同时除以$\frac{4}{5}$，即$x=20÷\frac{4}{5}$。
根据分数除法法则，除以一个分数等于乘以它的倒数，所以$x = 20×\frac{5}{4}=25$。
2. 对于方程$\frac{5}{12}x + 4 = 16$：
首先根据等式的性质，等式两边同时减去$4$，得到$\frac{5}{12}x+4 - 4=16 - 4$，即$\frac{5}{12}x = 12$。
然后等式两边同时除以$\frac{5}{12}$，$x = 12÷\frac{5}{12}$。
再根据分数除法法则，$x=12×\frac{12}{5}=\frac{144}{5}=28.8$。
3. 对于方程$\frac{2}{3}x+\frac{1}{5}x = 26$：
先通分，$\frac{2}{3}x+\frac{1}{5}x=\left(\frac{2×5}{3×5}+\frac{1×3}{5×3}\right)x=\left(\frac{10}{15}+\frac{3}{15}\right)x=\frac{13}{15}x$。
则原方程变为$\frac{13}{15}x = 26$。
根据等式的性质，等式两边同时除以$\frac{13}{15}$，$x = 26÷\frac{13}{15}$。
由分数除法法则，$x=26×\frac{15}{13}=30$。
【答案】：$x = 25$；$x = 28.8$；$x = 30$

四、画一画，涂一涂，算一算
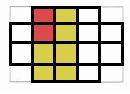
$\frac{2}{5}÷4=( )$

答案：
【解析】：
把一个长方形看作单位“$1$”，将其平均分成$5$份，取其中的$2$份表示$\frac{2}{5}$。再把这$\frac{2}{5}$平均分成$4$份，求其中一份是多少。
根据分数除法的计算方法：除以一个数（$0$除外）等于乘这个数的倒数，$\frac{2}{5}÷4=\frac{2}{5}×\frac{1}{4}$。
分子相乘：$2×1 = 2$；分母相乘：$5×4 = 20$，得到$\frac{2}{20}$，约分后为$\frac{1}{10}$。
【答案】：$\frac{1}{10}$

1. 某超市有进口水果120kg，恰好是国产水果的$\frac{4}{5}$。这个超市有国产水果多少千克？

答案： 【解析】：已知进口水果的重量是国产水果的$\frac{4}{5}$，即国产水果重量的$\frac{4}{5}$是120kg，求国产水果的重量，用除法计算，可列式为$120÷\frac{4}{5}$。根据分数除法的计算方法，除以一个分数等于乘以它的倒数，$120÷\frac{4}{5}=120×\frac{5}{4}=150$（千克）。
【答案】：150

2. 用一根$\frac{7}{15}$m长的铁丝做一个正方形，这个正方形的边长是多少米？面积是多少平方米？

答案： 【解析】：本题可根据正方形的周长和面积公式来求解。
**步骤一：求正方形的边长**
已知铁丝的长度为$\frac{7}{15}$米，用这根铁丝做正方形，那么铁丝的长度就是正方形的周长。
根据正方形的周长公式$C = 4a$（$C$表示周长，$a$表示边长），可得边长$a = C÷4$。
将$C = \frac{7}{15}$米代入公式，可得边长为$\frac{7}{15}÷4=\frac{7}{15}×\frac{1}{4}=\frac{7}{60}$（米）。
**步骤二：求正方形的面积**
根据正方形的面积公式$S = a^2$（$S$表示面积，$a$表示边长），将$a = \frac{7}{60}$米代入公式，可得面积为$(\frac{7}{60})^2=\frac{7}{60}×\frac{7}{60}=\frac{49}{3600}$（平方米）。
【答案】：边长是$\frac{7}{60}$米，面积是$\frac{49}{3600}$平方米。

3. 我国鸟类广泛分布于森林、草原、农田、居民点和各水域中，大约有1300种，约占全世界鸟类种数的$\frac{7}{50}$。全世界鸟类约有多少种？

答案： 【解析】：已知我国鸟类大约有1300种，约占全世界鸟类种数的$\frac{7}{50}$，把全世界鸟类种数看作单位“1”，求单位“1”的量，用除法计算，即全世界鸟类种数 = 我国鸟类种数÷我国鸟类种数占全世界鸟类种数的分率，列式为$1300÷\frac{7}{50}=1300×\frac{50}{7}=\frac{65000}{7}\approx9286$（种）。
【答案】：9286种