《2025年假期伙伴暑假大连理工大学出版社五年级数学北师大版》

1. 把体积是$1dm^{3}$的正方体木块切割成体积是$1cm^{3}$的小正方体，能切成(1000)块，把这些小正方体排成一行，长为(10)m。

答案： 1000，10

2. $40m^{3}=$($40000$)$dm^{3}$ $0.65L=$($650$)mL
$2100mL=$($2100$)$cm^{3}=$($2.1$)$dm^{3}$

答案： $40000$；$650$；$2100$；$2.1$

3. 一个正方体的棱长总和是$12dm$，它的体积是(1)$dm^{3}$。

答案： 1

4. 一个长方体的体积是$30cm^{3}$，长是$5cm$，高是$3cm$，宽是($2$)cm。

答案： $2$

5. 表面积是$54cm^{2}$的正方体，它的体积是($27$)$cm^{3}$。

答案： $27$

6. 一个长方体框架长$8cm$、宽$6cm$、高$4cm$，做这个框架共要(72cm)铁丝，是求长方体的(棱长总和)；在表面贴上塑料板共要(208$cm^{2}$)塑料板，是求长方体的(表面积)；在里面能盛(0.192)L水，是求长方体的(容积)；这个盒子有(0.192)$dm^{3}$，是求长方体的(体积)。

答案： 72cm，棱长总和；208$cm^{2}$，表面积；0.192，容积；0.192，体积

1. 从大到小排列。
$600mL$ $2060mL$ $7L$ $5970mL$ $70L$

答案： 【解析】：本题可先将不同单位的容积统一换算成以毫升（$mL$）为单位，再比较大小并从大到小排列。
因为$1L = 1000mL$，所以$7L=7×1000 = 7000mL$，$70L = 70×1000=70000mL$。
比较$70000$、$7000$、$5970$、$2060$、$600$的大小，可得$70000＞7000＞5970＞2060＞600$。
所以$70L＞7L＞5970mL＞2060mL＞600mL$。
【答案】：$70L＞7L＞5970mL＞2060mL＞600mL$

2. 从小到大排列。
$260mL$ $2060mL$ $2L$ $200mL$ $20L$

答案： 【解析】：本题可先将单位统一，再比较大小并进行排列。
因为$1L = 1000mL$，所以$2L=2×1000 = 2000mL$，$20L = 20×1000 = 20000mL$。
将$260mL$、$2060mL$、$2000mL$、$200mL$、$20000mL$按照从小到大的顺序排列为：$200mL＜260mL＜2000mL＜2060mL＜20000mL$，即$200mL＜260mL＜2L＜2060mL＜20L$。
【答案】：$200mL＜260mL＜2L＜2060mL＜20L$

三、算一算
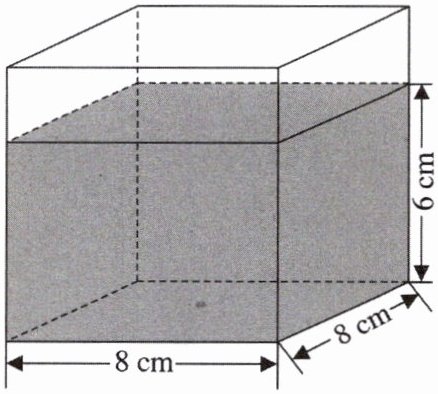
将一个铁球浸没在右图所示的水箱中后，水面上升到$7cm$处，求铁球的体积。铁球体积为$64cm^{3}$

答案： 【解析】：本题可根据铁球的体积等于上升的水的体积，利用长方体体积公式来求解。
- **步骤一：分析铁球体积与上升水的体积的关系**
当铁球浸没在水箱中时，水面上升的那部分水的体积就等于铁球的体积。
- **步骤二：计算水面上升的高度**
已知原来水面高度是$6cm$，放入铁球后水面上升到$7cm$，那么水面上升的高度为：$7 - 6=1cm$。
- **步骤三：计算上升的水的体积（即铁球的体积）**
水箱的底面是一个边长为$8cm$的正方形，根据长方体体积公式$V = a× b× h$（其中$V$为体积，$a$、$b$为长方体底面的长和宽，$h$为高），这里$a = b = 8cm$，水面上升的高度$h = 1cm$，则铁球的体积为：
$8×8×(7 - 6)$
$=8×8×1$
$=64×1$
$= 64cm^{3}$
【答案】：$64cm^{3}$