《2025年小学学霸作业本六年级数学上册人教版》

1.(名校期末真题)以半圆为弧的扇形的圆心角是(180)° ,圆心角是72°的扇形的面积是整个圆面积的$\frac{1}{5}$。

答案： 180 $\frac{1}{5}$

2. 下面图形中涂色部分是扇形的在( )里画“√”。 ( ) (√) ( ) ( ) (√) ( )
观察发现:在同一个圆中,扇形的大小只与扇形的(圆心角)的大小有关。

答案： （ ）（√）（ ）（ ）（√）（ ） 圆心角

3.[教材改编]画一个半径是2 cm的半圆,再在半圆中画一个圆心角是90° 的扇形,并求出扇形的周长和面积。

答案：

周长：$2×3.14×2×\frac{90}{360}+2×2=7.14(cm)$
面积：$3.14×2^{2}×\frac{90}{360}=3.14(cm^{2})$

4.[新趋势·学科融合]弧幕投影使画面更有冲击力且对眼睛更加友好。如图是弧幕投影的水平面内的原理图,单个镜头水平投影区域的面积是多少平方米?

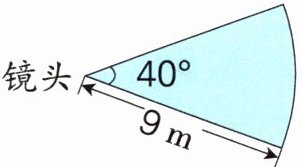
答案： $3.14×9^{2}×\frac{40}{360}=28.26(m^{2})$
答：单个镜头水平投影区域的面积是$28.26m^{2}$。

5.[新情境·传统文化]“数摺(zhé)聚清风,一捻生秋意。”描述的是我国传统折扇。一把折扇打开时的最大角度是${120}^{\circ }$,这把折扇的扇面面积是多少平方厘米?先将小净的思路补充完整,再类比求解。(得数保留整数)

若折扇打开为${180}^{\circ }$,则扇面面积相当于外圆半径为(20)cm、内圆半径为( ______ 12)cm的圆环面积的( ______ 一半)。

答案： 20 12 一半
$[3.14×20^{2}-3.14×(20-8)^{2}]×\frac{120}{360}\approx268(cm^{2})$
答：这把折扇的扇面面积是$268cm^{2}$。

6.求涂色部分の面积。
(1)三个圆的周长都是18.8 cm。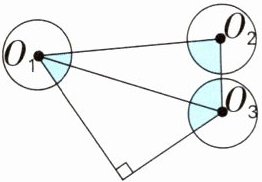
(2)8 dm

答案： （1）$18.84÷3.14÷2=3(cm)$
$3.14×3^{2}×\frac{180+90}{360}=21.195(cm^{2})$
解析：由图可知，涂色部分即所有扇形的半径都相等，而这些扇形的圆心角之和加$90^{\circ}$就等于2个三角形的内角和之和。
（2）$3.14×8^{2}×\frac{45}{360}-8×(8÷2)×\frac{1}{2}=9.12(dm^{2})$
解析：此题通过割补法进行解答，将半圆内右上方涂色部分移至左上方，求出圆心角为$45^{\circ}$、半径为$8dm$的扇形的面积，再减去三角形的面积即可。其中三角形的底等于半圆的直径，高等于半圆的半径。