第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 填空。
(1)剑鱼是海洋生物中游动速度比较快的一种鱼,每小时大约能游130 km。照这样计算,$\frac{2}{5}$小时能游(
(2)(名校期末真题)小明一家都很喜欢吃糍粑(cí bā),小明吃了$\frac{1}{5}$kg糍粑,妈妈比小明多吃了$\frac{1}{8}$,爸爸比小明多吃了$\frac{1}{8}$kg,妈妈吃了(
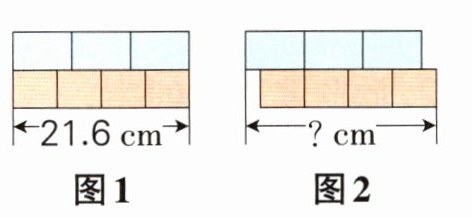
(3)亮亮先将两张同样长的长方形卡片分别等分成3份和4份(如图1),然后进行了重新拼摆(如图2),拼摆后的图形长(
(1)剑鱼是海洋生物中游动速度比较快的一种鱼,每小时大约能游130 km。照这样计算,$\frac{2}{5}$小时能游(
52
)km。(2)(名校期末真题)小明一家都很喜欢吃糍粑(cí bā),小明吃了$\frac{1}{5}$kg糍粑,妈妈比小明多吃了$\frac{1}{8}$,爸爸比小明多吃了$\frac{1}{8}$kg,妈妈吃了(
$\frac{9}{40}$
)kg,爸爸吃了($\frac{13}{40}$
)kg。(3)亮亮先将两张同样长的长方形卡片分别等分成3份和4份(如图1),然后进行了重新拼摆(如图2),拼摆后的图形长(
23.4
)cm。
答案:
1.
(1)52
(2)$\frac{9}{40}$ $\frac{13}{40}$
(3)23.4
(1)52
(2)$\frac{9}{40}$ $\frac{13}{40}$
(3)23.4
2. 选择。
(1)根据右边的线段图找出数量关系,正确的是(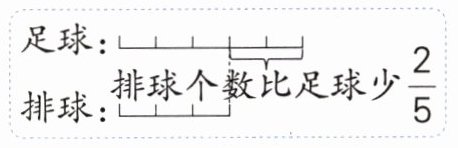
A. 足球个数×$(1 - \frac{2}{5})$= 排球个数
B. 足球个数×$(1 + \frac{2}{5})$= 排球个数
C. 排球个数×$(1 - \frac{2}{5})$= 足球个数
D. 排球个数×$(1 + \frac{2}{5})$= 足球个数
(2)[新趋势·算理探究]关于“$\frac{2}{7}×3= \frac{2×3}{7}= \frac{6}{7}$”,下面说法错误的是(
A. 分数乘整数,把分子和这个数相乘的积作分子,分母不变
B. 分母不变表示分数单位不变,分子和整数相乘的积表示分数单位的个数
C. $\frac{2}{7}×3= \frac{1}{7}×2×3= \frac{1}{7}×(2×3)= \frac{6}{7}$
D. $\frac{2}{7}×3= \frac{3+3}{7}= \frac{2×3}{7}= \frac{6}{7}$
(3)(符号意识)a和b在直线上的位置如下图所示,若$a×b= t$,则下列描述中正确的是(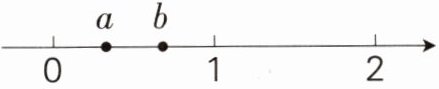
A. $a < b < t$
B. $a < t < b$
C. $t < a < b$
D. $t < b < a$
(1)根据右边的线段图找出数量关系,正确的是(
A
)。
A. 足球个数×$(1 - \frac{2}{5})$= 排球个数
B. 足球个数×$(1 + \frac{2}{5})$= 排球个数
C. 排球个数×$(1 - \frac{2}{5})$= 足球个数
D. 排球个数×$(1 + \frac{2}{5})$= 足球个数
(2)[新趋势·算理探究]关于“$\frac{2}{7}×3= \frac{2×3}{7}= \frac{6}{7}$”,下面说法错误的是(
D
)。A. 分数乘整数,把分子和这个数相乘的积作分子,分母不变
B. 分母不变表示分数单位不变,分子和整数相乘的积表示分数单位的个数
C. $\frac{2}{7}×3= \frac{1}{7}×2×3= \frac{1}{7}×(2×3)= \frac{6}{7}$
D. $\frac{2}{7}×3= \frac{3+3}{7}= \frac{2×3}{7}= \frac{6}{7}$
(3)(符号意识)a和b在直线上的位置如下图所示,若$a×b= t$,则下列描述中正确的是(
C
)。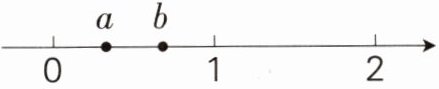
A. $a < b < t$
B. $a < t < b$
C. $t < a < b$
D. $t < b < a$
答案:
2.
(1)A
(2)D
(3)C
(1)A
(2)D
(3)C
3. 计算下面各题,能简算的要简算。
$\frac{7}{23}×5×\frac{23}{21}$
$15×(\frac{2}{15}+\frac{3}{11})×11$
$51×\frac{15}{52}$
$\frac{3}{4}×7.5+2.7×\frac{3}{4}-0.2×0.75$
$\frac{7}{23}×5×\frac{23}{21}$
$15×(\frac{2}{15}+\frac{3}{11})×11$
$51×\frac{15}{52}$
$\frac{3}{4}×7.5+2.7×\frac{3}{4}-0.2×0.75$
答案:
3.$\frac{7}{23}×5×\frac{23}{21}$ $15×(\frac{2}{15}+\frac{3}{11})×11$
$=\frac{7}{23}×\frac{23}{21}×5$ $=15×\frac{2}{15}×11+15×(\frac{3}{11}×11)$
$=\frac{1}{3}×5$ $=22+45$
$=\frac{5}{3}$ $=67$
$51×\frac{15}{52}$ $\frac{3}{4}×7.5+2.7×\frac{3}{4}-0.2×0.75$
$=(52-1)×\frac{15}{52}$ $=\frac{3}{4}×(7.5+2.7-0.2)$
$=52×\frac{15}{52}-1×\frac{15}{52}$ $=\frac{3}{4}×10$
$=14\frac{37}{52}$ $=\frac{15}{2}$
$=\frac{7}{23}×\frac{23}{21}×5$ $=15×\frac{2}{15}×11+15×(\frac{3}{11}×11)$
$=\frac{1}{3}×5$ $=22+45$
$=\frac{5}{3}$ $=67$
$51×\frac{15}{52}$ $\frac{3}{4}×7.5+2.7×\frac{3}{4}-0.2×0.75$
$=(52-1)×\frac{15}{52}$ $=\frac{3}{4}×(7.5+2.7-0.2)$
$=52×\frac{15}{52}-1×\frac{15}{52}$ $=\frac{3}{4}×10$
$=14\frac{37}{52}$ $=\frac{15}{2}$
查看更多完整答案,请扫码查看


