第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 选择。
(1)(名校期末真题)如图,求一共多少本,列式错误的是(
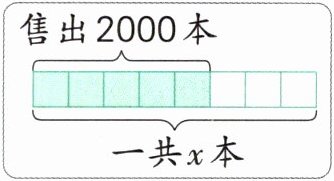
A. $2000×\left(1-\frac{3}{8}\right)$
B. $2000÷5×8$
C. $\frac{5}{8}x= 2000$
D. $2000÷\frac{5}{8}$
(2)下列问题中,不能用方程“$\left(1-\frac{1}{4}\right)x= 120$”解决的是(
A.
B.
C.
D.
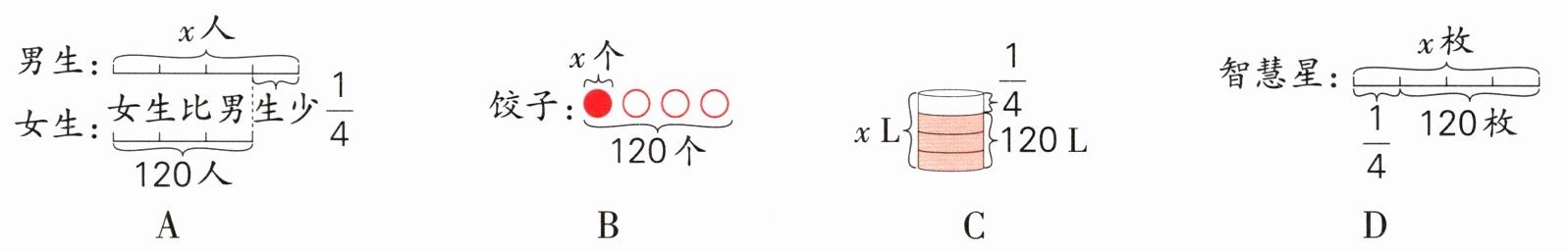
(1)(名校期末真题)如图,求一共多少本,列式错误的是(
A
)。
A. $2000×\left(1-\frac{3}{8}\right)$
B. $2000÷5×8$
C. $\frac{5}{8}x= 2000$
D. $2000÷\frac{5}{8}$
(2)下列问题中,不能用方程“$\left(1-\frac{1}{4}\right)x= 120$”解决的是(
B
)。A.
B.
C.
D.
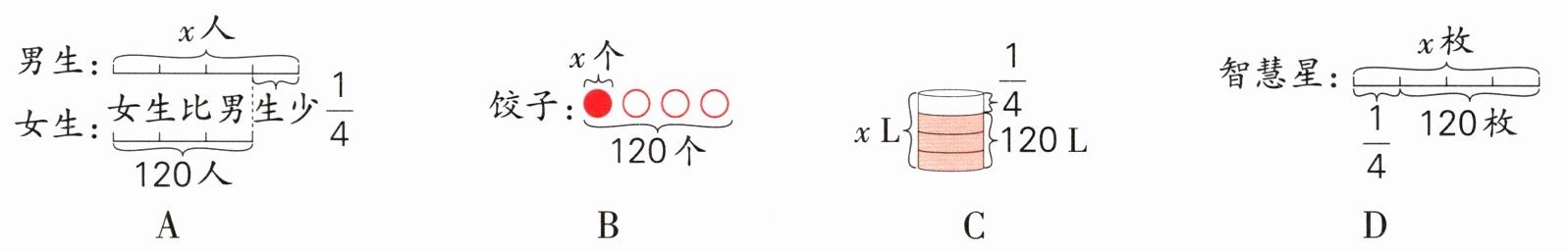
答案:
1.
(1)A
(2)B
(1)A
(2)B
2.[新情境·科技成就]“鸿鹄(hóng hú)”是我国首款配备“最强大脑”的全尺寸人形机器人整机产品。“鸿鹄”机器人身高为170 cm,比“镗钯(táng bǎ)”机器人高$\frac{10}{7}$。“镗钯”机器人身高为多少厘米?(先写出数量关系,再列方程求解)

答案:
“镗钯”机器人的身高×$(1+\frac {10}{7})$=“鸿鹄”机器人的身高
解:设“镗钯”机器人身高为x cm。
$(1+\frac {10}{7})x=170$ $x=70$
答:“镗钯”机器人身高为70 cm。
解:设“镗钯”机器人身高为x cm。
$(1+\frac {10}{7})x=170$ $x=70$
答:“镗钯”机器人身高为70 cm。
3.[教材改编]齐阿姨接到一批庆阳香包订单,2天完成了这批订单的$\frac{5}{12}$。照这样的速度,还要多少天才能完成这批订单?
答案:
$2÷\frac {5}{12}-2=\frac {14}{5}$(天)
答:还要$\frac {14}{5}$天才能完成这批订单。
答:还要$\frac {14}{5}$天才能完成这批订单。
4.[新趋势·材料阅读]一名10岁女生在校时,每天的最低饮水量约为多少毫升?
在校时,不同年龄的学生每天的最低饮水量不同:12岁女生的最低饮水量是10岁女生的$\frac{7}{6}$,12岁男生的最低饮水量比同年龄女生多$\frac{1}{7}$,约为800 mL。
在校时,不同年龄的学生每天的最低饮水量不同:12岁女生的最低饮水量是10岁女生的$\frac{7}{6}$,12岁男生的最低饮水量比同年龄女生多$\frac{1}{7}$,约为800 mL。
答案:
解:设每天的最低饮水量约为x mL。
$\frac {7}{6}x×(1+\frac {1}{7})=800$ $x=600$
答:每天的最低饮水量约为600 mL。
解析:由题可知,在校时,12岁女生每天的最低饮水量=10岁女生每天的最低饮水量×$\frac {7}{6}$,12岁男生每天的最低饮水量=12岁女生每天的最低饮水量×$(1+\frac {1}{7})$,据此求解。
$\frac {7}{6}x×(1+\frac {1}{7})=800$ $x=600$
答:每天的最低饮水量约为600 mL。
解析:由题可知,在校时,12岁女生每天的最低饮水量=10岁女生每天的最低饮水量×$\frac {7}{6}$,12岁男生每天的最低饮水量=12岁女生每天的最低饮水量×$(1+\frac {1}{7})$,据此求解。
查看更多完整答案,请扫码查看


