第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 选择。
(1)(名校期末真题)如图,将一个半径为6 cm的半圆平均分成8份,剪开后拼成一个近似的平行四边形,在这个转化过程中,下列说法正确的是(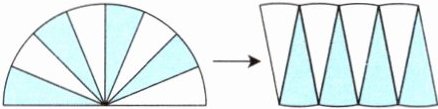
A. 面积和周长都没变
B. 面积变了,周长不变
C. 面积不变,周长变了
D. 面积和周长都变了
(2)如图,涂色部分的面积为(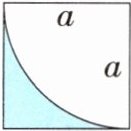
A. $a^{2}-\frac{1}{4}\pi a^{2}$
B. $a^{2}-\frac{1}{4}a^{2}$
C. $\frac{1}{4}(a^{2}-\pi a^{2})$
D. $a^{2}+\frac{1}{4}\pi a^{2}$
]
(1)(名校期末真题)如图,将一个半径为6 cm的半圆平均分成8份,剪开后拼成一个近似的平行四边形,在这个转化过程中,下列说法正确的是(
A
)。
A. 面积和周长都没变
B. 面积变了,周长不变
C. 面积不变,周长变了
D. 面积和周长都变了
(2)如图,涂色部分的面积为(
A
)。
A. $a^{2}-\frac{1}{4}\pi a^{2}$
B. $a^{2}-\frac{1}{4}a^{2}$
C. $\frac{1}{4}(a^{2}-\pi a^{2})$
D. $a^{2}+\frac{1}{4}\pi a^{2}$
]
答案:
1.
(1)A
(2)A
(1)A
(2)A
2.[新趋势·说理分析]超市举办投飞镖抽奖活动。如图,投中最中间的圆是一等奖,向外的圆环依次是二等奖、三等奖,剩余部分为四等奖。圆环的环宽都是1 dm。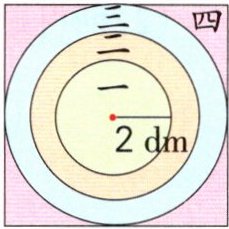
(1)萍萍:“二等奖和三等奖的环宽一样,中奖的可能性一样大。”她的说法(
(2)投中几等奖的可能性最大?请你计算说明。

(1)萍萍:“二等奖和三等奖的环宽一样,中奖的可能性一样大。”她的说法(
×
)(填“√”或“×”),理由:两个圆环内、外圆半径的平方差不相等(理由不唯一)
。(2)投中几等奖的可能性最大?请你计算说明。
一等奖:$3.14×2^{2}=12.56(dm^{2})$
二等奖:$3.14×[(2+1)^{2}-2^{2}]=15.7(dm^{2})$
三等奖:$3.14×[(2+1+1)^{2}-(2+1)^{2}]=21.98(dm^{2})$
四等奖:$(2+1+1)×2=8(dm)$
$8×8-3.14×(2+1+1)^{2}=13.76(dm^{2})$
$21.98>15.7>13.76>12.56$
答:投中三等奖的可能性最大。
二等奖:$3.14×[(2+1)^{2}-2^{2}]=15.7(dm^{2})$
三等奖:$3.14×[(2+1+1)^{2}-(2+1)^{2}]=21.98(dm^{2})$
四等奖:$(2+1+1)×2=8(dm)$
$8×8-3.14×(2+1+1)^{2}=13.76(dm^{2})$
$21.98>15.7>13.76>12.56$
答:投中三等奖的可能性最大。
答案:
2.
(1)× 两个圆环内、外圆半径的平方差不相等(理由不唯一)
(2)一等奖:$3.14×2^{2}=12.56(dm^{2})$
二等奖:$3.14×[(2+1)^{2}-2^{2}]=15.7(dm^{2})$
三等奖:$3.14×[(2+1+1)^{2}-(2+1)^{2}]=21.98(dm^{2})$
四等奖:$(2+1+1)×2=8(dm)$
$8×8-3.14×(2+1+1)^{2}=13.76(dm^{2})$
$21.98>15.7>13.76>12.56$
答:投中三等奖的可能性最大。
(1)× 两个圆环内、外圆半径的平方差不相等(理由不唯一)
(2)一等奖:$3.14×2^{2}=12.56(dm^{2})$
二等奖:$3.14×[(2+1)^{2}-2^{2}]=15.7(dm^{2})$
三等奖:$3.14×[(2+1+1)^{2}-(2+1)^{2}]=21.98(dm^{2})$
四等奖:$(2+1+1)×2=8(dm)$
$8×8-3.14×(2+1+1)^{2}=13.76(dm^{2})$
$21.98>15.7>13.76>12.56$
答:投中三等奖的可能性最大。
3.(名校期末真题)为了创建一个优美的居住环境,村部结合本村的实际情况准备在某居民组修建一个花坛,形状如图,它的边是4个直径相等的半圆。
(1)如果给花坛的周围围上栏杆,需要(
(2)这个花坛的面积是多少平方米?

(1)如果给花坛的周围围上栏杆,需要(
37.68
)m栏杆。(2)这个花坛的面积是多少平方米?
$6×6+3.14×(6÷2)^{2}÷2×4=92.52(m^{2})$
答:这个花坛的面积是$92.52m^{2}$。
答:这个花坛的面积是$92.52m^{2}$。
答案:
3.
(1)37.68
(2)$6×6+3.14×(6÷2)^{2}÷2×4=92.52(m^{2})$
答:这个花坛的面积是$92.52m^{2}$。
(1)37.68
(2)$6×6+3.14×(6÷2)^{2}÷2×4=92.52(m^{2})$
答:这个花坛的面积是$92.52m^{2}$。
4.[新情境·数学文化]《九章算术》中关于求圆形田面积的方法如下所示。
方法一:半周半径相乘得积步。译为:圆周长的一半乘半径为圆田面积。
方法二:周径相乘,四而一。译为:圆的周长乘直径,除以4。
方法三:径自相乘,三之,四而一。译为:圆的直径的平方,乘3,再除以4。
(1)现有圆形田,周长为30步,直径为10步,这块田的面积是多少平方步? 从上面任选一种方法列式解答:
(2)根据你选择的方法,说说这种方法与教材方法的关系,并说明理由。
方法一:半周半径相乘得积步。译为:圆周长的一半乘半径为圆田面积。
方法二:周径相乘,四而一。译为:圆的周长乘直径,除以4。
方法三:径自相乘,三之,四而一。译为:圆的直径的平方,乘3,再除以4。
(1)现有圆形田,周长为30步,直径为10步,这块田的面积是多少平方步? 从上面任选一种方法列式解答:
30÷2×(10÷2)=75(平方步)
。(2)根据你选择的方法,说说这种方法与教材方法的关系,并说明理由。
答案:
4.(答案不唯一)
(1)$30÷2×(10÷2)=75$(平方步)
(2)这种方法与教材方法的道理一致。
设圆的半径为r,周长为C,面积为S。
方法一:$C=2πr,C÷2×r=2πr÷2×r=πr^{2}=S,$
与教材方法一致。
(1)$30÷2×(10÷2)=75$(平方步)
(2)这种方法与教材方法的道理一致。
设圆的半径为r,周长为C,面积为S。
方法一:$C=2πr,C÷2×r=2πr÷2×r=πr^{2}=S,$
与教材方法一致。
查看更多完整答案,请扫码查看


