《2025年暑假作业八年级数学北师大版兰州大学出版社》

12. 如图11所示,已知线段AB,分别以A、B为圆心,大于AB一半的长为半径画弧,两弧相交于点C、Q,连接CQ,与AB相交于点D,连接AC,BC,AQ,BQ。
(1)求∠ADC的度数；
(2)当线段AB= 4,∠ACB= 60°时,△ABC的面积等于多少？

答案：
(1) 由作图可知，$CA=CB$，$QA=QB$，
$\therefore CQ$ 垂直平分 $AB$，
$\therefore \angle ADC=90^{\circ}$。
(2) $\because AC=CB$，$\angle ACB=60^{\circ}$，
$\therefore \triangle ABC$ 是等边三角形，
$\therefore AC=BC=AB=4$。
$\because CQ$ 垂直平分 $AB$，
$\therefore AD=\frac{1}{2}AB=2$，$\angle ADC=90^{\circ}$。
在 $\text{Rt}\triangle ADC$ 中，$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$。
$\therefore S_{\triangle ABC}=\frac{1}{2} × AB × CD=\frac{1}{2} × 4 × 2\sqrt{3}=4\sqrt{3}$。

13. 如图12所示,在△ABC中,∠C= 90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,垂足为F,连接DE。
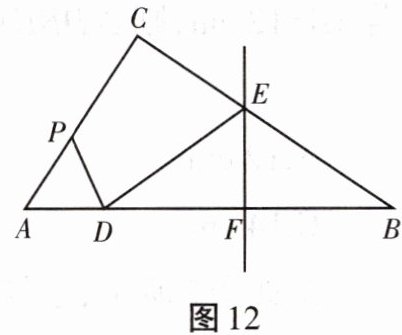
(1)判断DE与DP的位置关系,并说明理由。
(2)若AC= 5,BC= 7,PA= 2,求线段DE的长。

答案：

(1) $ DE \perp DP $, 理由如下: $ \because PD = PA $, $ \therefore \angle A = \angle PDA $, $ \because EF $ 是 $ BD $ 的垂直平分线, $ \therefore EB = ED $, $ \therefore \angle B = \angle EDB $, $ \because \angle C = 90^{\circ} $, $ \therefore \angle A + \angle B = 90^{\circ} $, $ \therefore \angle PDA + \angle EDB = 90^{\circ} $, $ \therefore \angle PDE = 180^{\circ} - 90^{\circ} = 90^{\circ} $, $ \therefore DE \perp DP $;
(2) 连接 $ PE $, 设 $ DE = x $, 则 $ EB = ED = x $, $ CE = 7 - x $, $ \because \angle C = \angle PDE = 90^{\circ} $, $ \therefore PC^{2} + CE^{2} = PE^{2} = PD^{2} + DE^{2} $, $ \therefore 3^{2} + (7 - x)^{2} = 2^{2} + x^{2} $, 解得: $ x = \frac{27}{7} $, 则 $ DE = \frac{27}{7} $.