《2025年暑假作业八年级数学北师大版兰州大学出版社》

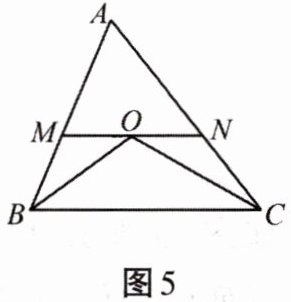
8. 如图5所示,已知BO平分$\angle CBA$,CO平分$\angle ACB$,$MN// BC$,且过点O,若$AB= 12$,$AC= 14$,则$\triangle AMN$的周长是______。

26

答案： 解：
∵ BO平分∠CBA，CO平分∠ACB，
∴ ∠ABO=∠CBO，∠ACO=∠BCO。
∵ MN//BC，
∴ ∠MOB=∠CBO，∠NOC=∠BCO。
∴ ∠ABO=∠MOB，∠ACO=∠NOC。
∴ MO=MB，NO=NC。
∵ △AMN的周长=AM+MO+NO+AN，
又
∵ MO=MB，NO=NC，
∴ △AMN的周长=AM+MB+AN+NC=AB+AC。
∵ AB=12，AC=14，
∴ △AMN的周长=12+14=26。
26

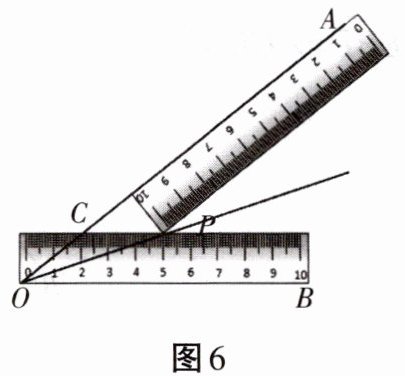
9. 如图6所示,小明将两把完全相同的长方形直尺放置在$\angle AOB$上,两把直尺的接触点为P,边OA与其中一把直尺边缘的交点为C,点C、P在这把直尺上的刻度读数分别是2、5,则OC的长度是______。

3 cm

答案： 解：由题意知，直尺刻度C为2，P为5，所以CP的长度为5 - 2 = 3。
因为两把直尺完全相同且放置在∠AOB上，接触点为P，根据角平分线的判定定理（到角两边距离相等的点在角的平分线上）及直尺的平行性质，可知OP为∠AOB的平分线，且OC = CP。
所以OC的长度是3 cm。
答案：3 cm

10. 作图题：(不写作法,但必须保留作图痕迹)
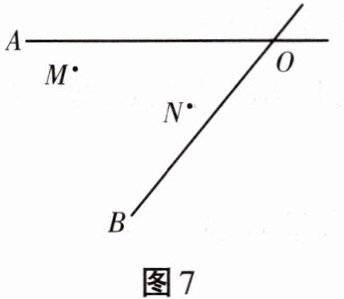
如图7所示,某地有两所大学和两条相交叉的公路(点M、N表示大学,AO、BO表示公路)。现计划在离大学更近的区域内修建一座物资仓库,使仓库到两所大学的距离相等,到两条公路的距离也相等。你能确定仓库P应该建在什么位置吗？用无刻度的直尺和圆规在所给的图形中画出你的设计方案。

答案：
如图所示：
(1) 连接 MN，分别以 M、N 为圆心，以大于 $\frac{1}{2}MN$ 的长为半径画弧，两弧相交于 D，E，连接 DE，则 DE 即为线段 MN 的垂直平分线；
(2) 以点 O 为圆心，以任意长为半径画弧，分别交 OA、OB 于 G、H，再分别以 G、H 为圆心，以大于 $\frac{1}{2}GH$ 的长为半径画弧，两弧相交于 F，作射线 OF，则 OF 即为 $\angle AOB$ 的平分线；
(3) DE 与 OF 相交于点 P，则点 P 即为所求。

11. 已知：如图8所示,AD是$\triangle ABC$的角平分线,$DE\bot AB$,$DF\bot AC$,垂足分别是E、F,$BD= CD$,求证：$\angle B= \angle C$。

答案： 证明：
∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF（角平分线上的点到角两边的距离相等）。
在Rt△DEB和Rt△DFC中，
$\left\{\begin{array}{l} BD=CD \\ DE=DF \end{array}\right.$，
∴Rt△DEB≌Rt△DFC（HL）。
∴∠B=∠C。

12. 如图9所示,已知在$\triangle ABC$中,$\angle C= 90^{\circ }$,点D是斜边AB的中点,$AB= 2BC$,$DE\bot AB$交AC于点E。
求证：BE平分$\angle ABC$。

答案： 证明：
∵ D 是 AB 的中点，
∴ $ BD = \frac{1}{2}AB $。
∵ $ AB = 2BC $，
∴ $ BC = \frac{1}{2}AB $，
∴ $ BD = BC $。
∵ $ DE \perp AB $，$ \angle C = 90^{\circ} $，
∴ $ \angle BDE = \angle C = 90^{\circ} $。
在 $ Rt\triangle BDE $ 和 $ Rt\triangle BCE $ 中，
$ \begin{cases} BE = BE \\ BD = BC \end{cases} $
∴ $ Rt\triangle BDE \cong Rt\triangle BCE(HL) $，
∴ $ \angle DBE = \angle EBC $，
∴ BE 平分 $ \angle ABC $。