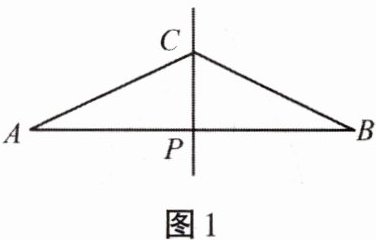
1. 如图1所示,直线CP是AB的中垂线且交AB于点P,其中AP= 2CP。甲、乙两人想在AB上取两点D、E,使得AD= DC= CE= EB,其作法如下:
(甲)作∠ACP、∠BCP的角平分线,分别交AB于点D、E,则D、E即为所求;
(乙)作AC、BC的中垂线,分别交AB于点D、E,则D、E即为所求。
对于甲、乙两人的作法,下列判断正确的是 (
A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确

(甲)作∠ACP、∠BCP的角平分线,分别交AB于点D、E,则D、E即为所求;
(乙)作AC、BC的中垂线,分别交AB于点D、E,则D、E即为所求。
对于甲、乙两人的作法,下列判断正确的是 (
D
)A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确
答案:
设 $ CP = x $,则 $ AP = 2x $,$ AB = 4x $,$ AC = \sqrt{(2x)^2 + x^2} = \sqrt{5}x $。
甲的作法:
假设 $ D $ 是 $ \angle ACP $ 角平分线与 $ AB $ 的交点,由角平分线定理得 $ \frac{AD}{DP} = \frac{AC}{CP} = \sqrt{5} $。设 $ DP = m $,则 $ AD = \sqrt{5}m $,$ AP = AD + DP = (\sqrt{5} + 1)m = 2x $,解得 $ m = \frac{2x}{\sqrt{5} + 1} $,$ AD = \frac{2\sqrt{5}x}{\sqrt{5} + 1} $。
计算 $ DC $:在 $ \triangle DCP $ 中,$ DC = \sqrt{DP^2 + CP^2} = \sqrt{m^2 + x^2} \neq AD $,故甲错误。
乙的作法:
设 $ AC $ 中垂线交 $ AB $ 于 $ D $,则 $ AD = DC $。设 $ AD = DC = n $,$ DP = 2x - n $,在 $ \triangle DCP $ 中,$ DC^2 = DP^2 + CP^2 $,即 $ n^2 = (2x - n)^2 + x^2 $,解得 $ n = \frac{5x}{4} $,满足 $ AD = DC $。同理,$ CE = EB $ 成立,故乙正确。
结论: 甲错误,乙正确。
答案:D
甲的作法:
假设 $ D $ 是 $ \angle ACP $ 角平分线与 $ AB $ 的交点,由角平分线定理得 $ \frac{AD}{DP} = \frac{AC}{CP} = \sqrt{5} $。设 $ DP = m $,则 $ AD = \sqrt{5}m $,$ AP = AD + DP = (\sqrt{5} + 1)m = 2x $,解得 $ m = \frac{2x}{\sqrt{5} + 1} $,$ AD = \frac{2\sqrt{5}x}{\sqrt{5} + 1} $。
计算 $ DC $:在 $ \triangle DCP $ 中,$ DC = \sqrt{DP^2 + CP^2} = \sqrt{m^2 + x^2} \neq AD $,故甲错误。
乙的作法:
设 $ AC $ 中垂线交 $ AB $ 于 $ D $,则 $ AD = DC $。设 $ AD = DC = n $,$ DP = 2x - n $,在 $ \triangle DCP $ 中,$ DC^2 = DP^2 + CP^2 $,即 $ n^2 = (2x - n)^2 + x^2 $,解得 $ n = \frac{5x}{4} $,满足 $ AD = DC $。同理,$ CE = EB $ 成立,故乙正确。
结论: 甲错误,乙正确。
答案:D
2. 如图2所示,在Rt△ABC中,∠C= 90°,∠B= 30°。AB的垂直平分线DE交AB于点D,交BC于点E,则下列结论不正确的是 (
A.AE= BE
B.AC= BE
C.CE= DE
D.∠CAE= ∠B
B
)A.AE= BE
B.AC= BE
C.CE= DE
D.∠CAE= ∠B
答案:
解:
∵DE是AB的垂直平分线,
∴AE=BE(垂直平分线上的点到线段两端距离相等),A正确;
在Rt△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,AE=BE,
∴∠EAB=∠B=30°,
∴∠CAE=∠CAB-∠EAB=30°=∠B,D正确;
在Rt△ACE和Rt△ADE中,
∠CAE=∠DAE=30°,AE=AE,
∴Rt△ACE≌Rt△ADE(AAS),
∴CE=DE,C正确;
AC=BC·tan30°=BC·√3/3,BE=BC-CE,无法直接得出AC=BE,B不正确。
结论:B
∵DE是AB的垂直平分线,
∴AE=BE(垂直平分线上的点到线段两端距离相等),A正确;
在Rt△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,AE=BE,
∴∠EAB=∠B=30°,
∴∠CAE=∠CAB-∠EAB=30°=∠B,D正确;
在Rt△ACE和Rt△ADE中,
∠CAE=∠DAE=30°,AE=AE,
∴Rt△ACE≌Rt△ADE(AAS),
∴CE=DE,C正确;
AC=BC·tan30°=BC·√3/3,BE=BC-CE,无法直接得出AC=BE,B不正确。
结论:B
3. 如图3所示,是一块三角形草坪,现要在草坪上建一凉亭供大家休息,使凉亭到草坪三条边的距离相等,凉亭的位置应选在 (
A.△ABC三条中线的交点
B.△ABC三边中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
C
)A.△ABC三条中线的交点
B.△ABC三边中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
答案:
要使凉亭到三角形草坪三条边的距离相等,根据角平分线的性质:角平分线上的点到角两边的距离相等。三角形三条角平分线的交点到三角形三边的距离相等。所以凉亭的位置应选在△ABC三条角平分线的交点。
C
C
4. 如图4所示,AC= AD,BC= BD,则有 (
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
A
)A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
答案:
解:在△ACB和△ADB中,
∵AC=AD,BC=BD,AB=AB,
∴△ACB≌△ADB(SSS),
∴∠CAB=∠DAB,∠CBA=∠DBA,
即AB是∠CAD和∠CBD的平分线。
在△ACO和△ADO中(O为AB与CD交点),
∵AC=AD,∠CAO=∠DAO,AO=AO,
∴△ACO≌△ADO(SAS),
∴CO=DO,∠AOC=∠AOD=90°,
∴AB垂直平分CD。
答案:A
∵AC=AD,BC=BD,AB=AB,
∴△ACB≌△ADB(SSS),
∴∠CAB=∠DAB,∠CBA=∠DBA,
即AB是∠CAD和∠CBD的平分线。
在△ACO和△ADO中(O为AB与CD交点),
∵AC=AD,∠CAO=∠DAO,AO=AO,
∴△ACO≌△ADO(SAS),
∴CO=DO,∠AOC=∠AOD=90°,
∴AB垂直平分CD。
答案:A
5. 如图5所示,∠ABC= 50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是
115°
。
答案:
解:
∵AD垂直且平分BC,
∴EB=EC,∠EDB=∠EDC=90°,BD=CD。
∵BE平分∠ABC,∠ABC=50°,
∴∠EBD=∠ABC/2=25°。
在Rt△EDB中,∠BED=90°-∠EBD=65°。
∵∠BED+∠DEC=180°,
∴∠DEC=180°-65°=115°。
∵EB=EC,ED⊥BC,
∴∠AEB=∠AEC(三线合一)。
又
∵∠AEB=∠DEC(对顶角相等),
∴∠AEC=∠DEC=115°。
答案:115°
∵AD垂直且平分BC,
∴EB=EC,∠EDB=∠EDC=90°,BD=CD。
∵BE平分∠ABC,∠ABC=50°,
∴∠EBD=∠ABC/2=25°。
在Rt△EDB中,∠BED=90°-∠EBD=65°。
∵∠BED+∠DEC=180°,
∴∠DEC=180°-65°=115°。
∵EB=EC,ED⊥BC,
∴∠AEB=∠AEC(三线合一)。
又
∵∠AEB=∠DEC(对顶角相等),
∴∠AEC=∠DEC=115°。
答案:115°
查看更多完整答案,请扫码查看


