搜索
11. 下列图形中,绕某个点旋转$180^{\circ}$能与自身重合的有(
①正方形；②长方形；③等边三角形；④线段；⑤角；⑥平行四边形.
A.5个
B.4个
C.3个
D.2个
B
)①正方形；②长方形；③等边三角形；④线段；⑤角；⑥平行四边形.
A.5个
B.4个
C.3个
D.2个
答案：
解：①正方形绕对角线交点旋转180°能与自身重合；
②长方形绕对角线交点旋转180°能与自身重合；
③等边三角形绕中心旋转180°不能与自身重合；
④线段绕中点旋转180°能与自身重合；
⑤角绕顶点旋转180°不能与自身重合；
⑥平行四边形绕对角线交点旋转180°能与自身重合。
能重合的有①②④⑥，共4个。
答案：B
②长方形绕对角线交点旋转180°能与自身重合；
③等边三角形绕中心旋转180°不能与自身重合；
④线段绕中点旋转180°能与自身重合；
⑤角绕顶点旋转180°不能与自身重合；
⑥平行四边形绕对角线交点旋转180°能与自身重合。
能重合的有①②④⑥，共4个。
答案：B
12. 关于轴对称位置变换,说法正确的有(
①对应线段平行且相等；
②对应点所连的线段被对称轴垂直平分；
③对应角相等；
④轴对称得到的图形与原图形全等.
A.1个
B.2个
C.3个
D.4个
C
)①对应线段平行且相等；
②对应点所连的线段被对称轴垂直平分；
③对应角相等；
④轴对称得到的图形与原图形全等.
A.1个
B.2个
C.3个
D.4个
答案：
解：①对应线段相等，但不一定平行，错误；
②对应点所连的线段被对称轴垂直平分，正确；
③对应角相等，正确；
④轴对称得到的图形与原图形全等，正确。
正确的有②③④，共3个。
答案：C
②对应点所连的线段被对称轴垂直平分，正确；
③对应角相等，正确；
④轴对称得到的图形与原图形全等，正确。
正确的有②③④，共3个。
答案：C
13. 将图6中的图形向右平移5格,再向下平移2格.
答案：
【解析】：
本题主要考查图形在方格纸上的平移变换，需要掌握图形平移的基本方法，即先确定图形各个顶点的位置，然后按照平移的要求分别移动各个顶点，最后连接移动后的顶点得到平移后的图形。
【答案】：
解：
1. 首先确定原图形各个顶点的位置，假设左下角顶点为$A$，按逆时针方向依次标记为$B$、$C$、$D$。
2. 将各个顶点向右平移$5$格，得到新的顶点$A_1$、$B_1$、$C_1$、$D_1$。
3. 再将$A_1$、$B_1$、$C_1$、$D_1$向下平移$2$格，得到最终的顶点$A_2$、$B_2$、$C_2$、$D_2$。
4. 依次连接$A_2$、$B_2$、$C_2$、$D_2$，得到平移后的图形。
图略。
本题主要考查图形在方格纸上的平移变换，需要掌握图形平移的基本方法，即先确定图形各个顶点的位置，然后按照平移的要求分别移动各个顶点，最后连接移动后的顶点得到平移后的图形。
【答案】：
解：
1. 首先确定原图形各个顶点的位置，假设左下角顶点为$A$，按逆时针方向依次标记为$B$、$C$、$D$。
2. 将各个顶点向右平移$5$格，得到新的顶点$A_1$、$B_1$、$C_1$、$D_1$。
3. 再将$A_1$、$B_1$、$C_1$、$D_1$向下平移$2$格，得到最终的顶点$A_2$、$B_2$、$C_2$、$D_2$。
4. 依次连接$A_2$、$B_2$、$C_2$、$D_2$，得到平移后的图形。
图略。
14. 如图7所示,在平面直角坐标系中,$\triangle AOB的顶点坐标分别是A(2,2)$,$O(0,0)$,$B(3,0)$,按要求完成下列问题.
(1)将$\triangle AOB$向左平移2个单位长度得到$\triangle A_{1}O_{1}B_{1}$,直接写出点$A_{1}$、$O_{1}$、$B_{1}$的坐标；
(2)将$\triangle AOB绕点A顺时针旋转90^{\circ}得到\triangle AO_{2}B_{2}$,画出$\triangle AO_{2}B_{2}$,并写出$O_{2}$、$B_{2}$的坐标；
(3)点$C的坐标为(-4,1)$,在$x轴上确定一点M$,使$AM + CM$最小,并写出点$M$的坐标.
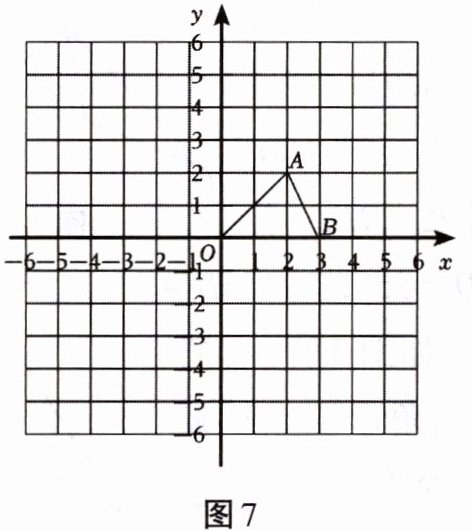
(1)将$\triangle AOB$向左平移2个单位长度得到$\triangle A_{1}O_{1}B_{1}$,直接写出点$A_{1}$、$O_{1}$、$B_{1}$的坐标；
(2)将$\triangle AOB绕点A顺时针旋转90^{\circ}得到\triangle AO_{2}B_{2}$,画出$\triangle AO_{2}B_{2}$,并写出$O_{2}$、$B_{2}$的坐标；
(3)点$C的坐标为(-4,1)$,在$x轴上确定一点M$,使$AM + CM$最小,并写出点$M$的坐标.
答案：
(1) $A_1(0,2)$，$O_1(-2,0)$，$B_1(1,0)$
(2) 图略，$O_2(0,4)$，$B_2(0,1)$
(3) $M(-2,0)$
(1) $A_1(0,2)$，$O_1(-2,0)$，$B_1(1,0)$
(2) 图略，$O_2(0,4)$，$B_2(0,1)$
(3) $M(-2,0)$
15. 如图8所示,已知点$O是\triangle ABC边AC$的中点,试画出
$\triangle ABC绕点O旋转180^{\circ}$后得到的图形,得到的图形和原来的图形组成什么图形？
$\triangle ABC绕点O旋转180^{\circ}$后得到的图形,得到的图形和原来的图形组成什么图形？
答案：
解：作图如下（此处省略作图过程，实际作答时需按要求画出图形）。得到的图形和原来的图形组成平行四边形。
16. 钟表上的时针、分针和秒针都在绕钟表中心做旋转运动.
(1)钟表从2时开始,经过20分钟后,分针和时针分别旋转了多少度？
(2)当时间到$3:20$时,钟表上时针和分针的夹角是多少度？
(1)钟表从2时开始,经过20分钟后,分针和时针分别旋转了多少度？
(2)当时间到$3:20$时,钟表上时针和分针的夹角是多少度？
答案：
(1) 解：分针每分钟旋转的角度为 $360^{\circ} ÷ 60 = 6^{\circ}$，20分钟旋转了 $6^{\circ} × 20 = 120^{\circ}$；时针每小时旋转 $360^{\circ} ÷ 12 = 30^{\circ}$，每分钟旋转 $30^{\circ} ÷ 60 = 0.5^{\circ}$，20分钟旋转了 $0.5^{\circ} × 20 = 10^{\circ}$。
(2) 解：3点时，时针与分针的夹角为 $30^{\circ} × 3 = 90^{\circ}$；20分钟内，分针旋转了 $6^{\circ} × 20 = 120^{\circ}$，时针旋转了 $0.5^{\circ} × 20 = 10^{\circ}$；此时夹角为 $|90^{\circ} + 10^{\circ} - 120^{\circ}| = 20^{\circ}$。
(1) 分针旋转了 $120^{\circ}$，时针旋转了 $10^{\circ}$；
(2) $20^{\circ}$
(1) 解：分针每分钟旋转的角度为 $360^{\circ} ÷ 60 = 6^{\circ}$，20分钟旋转了 $6^{\circ} × 20 = 120^{\circ}$；时针每小时旋转 $360^{\circ} ÷ 12 = 30^{\circ}$，每分钟旋转 $30^{\circ} ÷ 60 = 0.5^{\circ}$，20分钟旋转了 $0.5^{\circ} × 20 = 10^{\circ}$。
(2) 解：3点时，时针与分针的夹角为 $30^{\circ} × 3 = 90^{\circ}$；20分钟内，分针旋转了 $6^{\circ} × 20 = 120^{\circ}$，时针旋转了 $0.5^{\circ} × 20 = 10^{\circ}$；此时夹角为 $|90^{\circ} + 10^{\circ} - 120^{\circ}| = 20^{\circ}$。
(1) 分针旋转了 $120^{\circ}$，时针旋转了 $10^{\circ}$；
(2) $20^{\circ}$
查看更多完整答案，请扫码查看
