《2025年暑假作业八年级数学北师大版兰州大学出版社》

1. 下列不等式中,是一元一次不等式的有(B)
①$x＞-3$；②$xy≥1$；③$x^{2}＜3$；④$\frac {x}{2}-\frac {x}{3}≤1$；⑤$\frac {x+1}{x}＞1$.
A.1个
B.2个
C.3个
D.4个

答案： 解：①$x＞-3$，是一元一次不等式；
②$xy≥1$，含有两个未知数，不是一元一次不等式；
③$x^{2}＜3$，未知数的次数是2，不是一元一次不等式；
④$\frac {x}{2}-\frac {x}{3}≤1$，是一元一次不等式；
⑤$\frac {x+1}{x}＞1$，分母含有未知数，不是一元一次不等式。
综上，是一元一次不等式的有①④，共2个。
答案：B

2. 不等式$3(x-2)≤x+4$的非负整数解有(C)
A.4个
B.5个
C.6个
D.无数个

答案： 解：$3(x-2)≤x+4$
$3x-6≤x+4$
$3x-x≤4+6$
$2x≤10$
$x≤5$
非负整数解为：0，1，2，3，4，5，共6个。
C

3. 不等式$4x-\frac {1}{4}\lt x+\frac {11}{4}$的最大整数解为(B)
A.1
B.0
C.-1
D.不存在

答案： 解：$4x - \frac{1}{4} ＜ x + \frac{11}{4}$
$4x - x ＜ \frac{11}{4} + \frac{1}{4}$
$3x ＜ 3$
$x ＜ 1$
所以不等式的最大整数解为 $0$。
答案：B

4. 与$2x＜6$不同解的不等式是(D)
A.$2x+1＜7$
B.$4x＜12$
C.$-4x＞-12$
D.$-2x＜-6$

答案： 解：解不等式$2x＜6$，得$x＜3$。
A. 解不等式$2x + 1＜7$，$2x＜6$，得$x＜3$，与原不等式同解。
B. 解不等式$4x＜12$，得$x＜3$，与原不等式同解。
C. 解不等式$-4x＞ -12$，两边同时除以$-4$，不等号变向，得$x＜3$，与原不等式同解。
D. 解不等式$-2x＜ -6$，两边同时除以$-2$，不等号变向，得$x＞3$，与原不等式不同解。
答案：D

5. 不等式$ax+b＞0(a＜0)$的解集是(B)
A.$x＞-\frac {b}{a}$
B.$x＜-\frac {b}{a}$
C.$x＞\frac {b}{a}$
D.$x＜\frac {b}{a}$

答案： 解：$ax + b ＞ 0$
移项得：$ax ＞ -b$
因为 $a ＜ 0$，不等式两边同时除以 $a$，不等号方向改变，
所以 $x ＜ -\frac{b}{a}$
答案：B

6. 如果不等式$(m-2)x＞2-m$的解集是$x＜-1$,则有(B)
A.$m＞2$
B.$m＜2$
C.$m= 2$
D.$m≠2$

答案： 解：因为不等式$(m - 2)x＞2 - m$的解集是$x＜ - 1$，
不等式两边同时除以$(m - 2)$后不等号方向改变，
所以$m - 2＜0$，
解得$m＜2$。
答案：B

7. 若关于$x的方程3x+2m= 2$的解是正数,则$m$的取值范围是(B)
A.$m＞1$
B.$m＜1$
C.$m≥1$
D.$m≤1$

答案： 解：解方程$3x + 2m = 2$，得$x=\frac{2-2m}{3}$。
因为方程的解是正数，所以$\frac{2-2m}{3}＞0$。
两边同乘3，得$2 - 2m＞0$。
移项，得$-2m＞-2$。
两边同除以$-2$，得$m＜1$。
答案：B

8. 已知$(y-3)^{2}+|2y-4x-a|= 0$,若$x$为负数,则$a$的取值范围是(D)
A.$a＞3$
B.$a＞4$
C.$a＞5$
D.$a＞6$

答案： 解：因为$(y - 3)^2 + |2y - 4x - a| = 0$，且$(y - 3)^2 \geq 0$，$|2y - 4x - a| \geq 0$，所以$y - 3 = 0$，$2y - 4x - a = 0$。
由$y - 3 = 0$，得$y = 3$。
将$y = 3$代入$2y - 4x - a = 0$，得$6 - 4x - a = 0$，解得$x = \frac{6 - a}{4}$。
因为$x$为负数，所以$\frac{6 - a}{4} ＜ 0$，即$6 - a ＜ 0$，解得$a ＞ 6$。
D

9. 当$x$≤5时,代数式$\frac {x+3}{2}-\frac {5x-1}{6}$的值是非负数.

答案： 解：由题意得$\frac{x + 3}{2}-\frac{5x - 1}{6}\geq0$
去分母，得$3(x + 3)-(5x - 1)\geq0$
去括号，得$3x + 9 - 5x + 1\geq0$
合并同类项，得$-2x + 10\geq0$
移项，得$-2x\geq -10$
系数化为1，得$x\leq5$
≤5

10. 当代数式$\frac {x}{2}-3$的值大于10时,$x$的取值范围是$x＞26$.

答案： 解：由题意得$\frac{x}{2} - 3 ＞ 10$
$\frac{x}{2} ＞ 10 + 3$
$\frac{x}{2} ＞ 13$
$x ＞ 26$
x＞26

11. 若代数式$\frac {3(k+5)}{2}$的值不大于代数式5k-1的值,则$k$的取值范围是$k \geq \frac{17}{7}$.

答案： 解：由题意得$\frac{3(k + 5)}{2} \leq 5k - 1$
两边同乘2：$3(k + 5) \leq 2(5k - 1)$
去括号：$3k + 15 \leq 10k - 2$
移项：$3k - 10k \leq -2 - 15$
合并同类项：$-7k \leq -17$
系数化为1：$k \geq \frac{17}{7}$
$k$的取值范围是$k \geq \frac{17}{7}$

12. 若不等式$3x-m≤0$的正整数解是1,2,3,则$m$的取值范围是$9 \leq m ＜ 12$.

答案： 解：解不等式$3x - m \leq 0$，得$x \leq \frac{m}{3}$。
因为不等式的正整数解是1，2，3，所以$3 \leq \frac{m}{3} ＜ 4$，解得$9 \leq m ＜ 12$。
$9 \leq m ＜ 12$

13. 若关于$x的方程2x-6= -a$的解为负数,实数$a$的取值范围是$a＞6$.

答案： 解：解方程$2x - 6=-a$，得$2x=6 - a$，$x=\frac{6 - a}{2}$。
因为方程的解为负数，所以$\frac{6 - a}{2}＜0$，解得$6 - a＜0$，$a＞6$。
故实数$a$的取值范围是$a＞6$。

14. 解下列不等式,并把解集在数轴上表示出来：
(1)$-x+1≤7x-3$；
(2)$\frac {x+1}{7}＞x-5$.

答案：

(1)x≥1/2

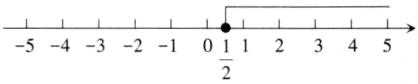
(2)x＜6