《2025年暑假作业八年级数学北师大版兰州大学出版社》

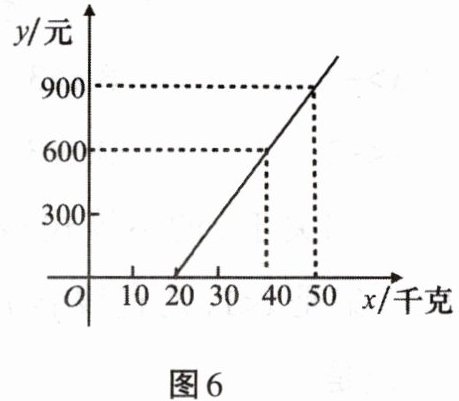
8. 如图6,某航空公司托运行李的费用与托运行李的质量的关系为一次函数,由图6可知行李的质量只要不超过20千克,就可以免费托运。

答案： 解：设一次函数解析式为$y = kx + b$。
由图可知，函数图像过点$(40, 600)$和$(50, 900)$，代入得：
$\begin{cases}40k + b = 600 \\50k + b = 900\end{cases}$
解得：$k = 30$，$b = -600$，即$y = 30x - 600$。
免费托运时$y = 0$，则$30x - 600 = 0$，解得$x = 20$。
20

9. 当自变量$x$$＞ -\frac{4}{5}$时,函数$y= 5x+4$的值大于0；当$x$$＜ -\frac{4}{5}$时,函数$y= 5x+4$的值小于0。

答案： 解：当函数值大于0时，$5x + 4 ＞ 0$，解得$x ＞ -\frac{4}{5}$；当函数值小于0时，$5x + 4 ＜ 0$，解得$x ＜ -\frac{4}{5}$。
$x ＞ -\frac{4}{5}$；$x ＜ -\frac{4}{5}$

10. 已知$2x-y= 0$,且$x-5＞y$,则$x$的取值范围是$x ＜ -5$。

答案： 解：由$2x - y = 0$，得$y = 2x$。
将$y = 2x$代入$x - 5 ＞ y$，得$x - 5 ＞ 2x$。
移项，得$x - 2x ＞ 5$。
合并同类项，得$-x ＞ 5$。
系数化为$1$，得$x ＜ -5$。
$x ＜ -5$

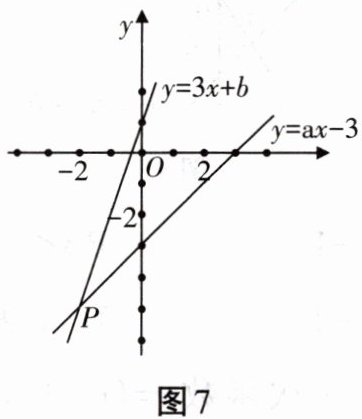
11. 如图7所示,已知函数$y= 3x+b和y= ax-3的图象交于点P(-2,-5)$,则根据图象可得不等式$3x+b＞ax-3$的解集是$x ＞ -2$。

答案： 因为函数$y = 3x + b$和$y = ax - 3$的图象交于点$P(-2,-5)$，从图象可以看出，当$x ＞ -2$时，函数$y = 3x + b$的图象在函数$y = ax - 3$的图象上方，所以不等式$3x + b ＞ ax - 3$的解集是$x ＞ -2$。
$x ＞ -2$

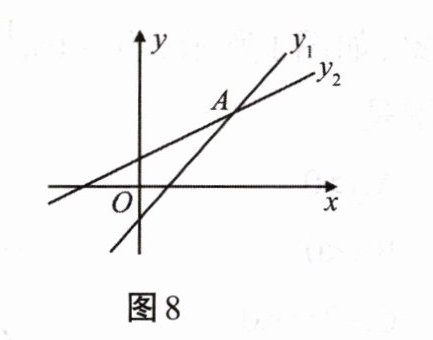
12. 如图8所示,一次函数$y_{1}= k_{1}x+b_{1}与y_{2}= k_{2}x+b_{2}$的图象相交于点A(3,2),则不等式$(k_{2}-k_{1})x+b_{2}-b_{1}＞0$的解集为$x＜3$。

答案： 解：由题意知，一次函数$y_{1}=k_{1}x+b_{1}$与$y_{2}=k_{2}x+b_{2}$的图象相交于点$A(3,2)$。
不等式$(k_{2}-k_{1})x + b_{2}-b_{1}＞0$可变形为$k_{2}x + b_{2}＞k_{1}x + b_{1}$，即$y_{2}＞y_{1}$。
观察函数图象，当$x＜3$时，$y_{2}$的图象在$y_{1}$的图象上方，此时$y_{2}＞y_{1}$。
所以不等式$(k_{2}-k_{1})x + b_{2}-b_{1}＞0$的解集为$x＜3$。
$x＜3$

13. 在同一坐标系中画出一次函数$y_{1}= -x+1与y_{2}= 2x-2$的图象,并根据图象回答下列问题：
(1)写出直线$y_{1}= -x+1与y_{2}= 2x-2的交点P$的坐标。
(2)直接写出：当$x$取何值时,$y_{1}＞y_{2}$；$y_{1}＜y_{2}$。

答案： 解：画图如下（此处略去画图步骤，实际答题时需在坐标系中描点连线画出两个函数图象）
(1) 联立方程：$\begin{cases}y = -x + 1 \\ y = 2x - 2\end{cases}$
将$y = -x + 1$代入$y = 2x - 2$得：$-x + 1 = 2x - 2$
解得$x = 1$，代入$y = -x + 1$得$y = 0$，所以交点$P(1, 0)$
(2) 当$x ＜ 1$时，$y_1 ＞ y_2$；当$x ＞ 1$时，$y_1 ＜ y_2$