《2025年暑假作业八年级数学北师大版兰州大学出版社》

8. 下列图形中,是由(1)仅通过平移得到的是(C)

答案： 平移不改变图形的形状、大小和方向。观察各选项：
- A选项图形方向改变，不符合平移性质；
- B选项图形形状与原图形不同，不符合平移性质；
- C选项图形形状、大小和方向均与原图形一致，符合平移性质；
- D选项图形方向改变，不符合平移性质。
答案：C

9. 如图7所示,图形旋转一定角度后能与自身重合,则旋转的角度可能是(C)
A.$30^{\circ }$
B.$60^{\circ }$
C.$90^{\circ }$
D.$120^{\circ }$

答案： 观察图形，该图形为旋转对称图形。由图可知，图形被平均分成4个全等部分，所以最小旋转角为$360^{\circ}÷4 = 90^{\circ}$，旋转$90^{\circ}$后能与自身重合。
答案：C

10. 如图8所示,面积为$12cm^{2}的\triangle ABC$沿BC方向平移至$\triangle DEF$的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为(B)
A.$24cm^{2}$
B.$36cm^{2}$
C.$48cm^{2}$
D.无法确定

答案： 解：设BC长为$x$，$\triangle ABC$的BC边上的高为$h$。
由$\triangle ABC$面积为$12cm^2$，得$\frac{1}{2}xh = 12$，即$xh = 24$。
平移距离为BC长的两倍，即$BE = 2x$，则$CE = BE - BC = 2x - x = x$。
四边形ACED为梯形，上底$CE = x$，下底$AD = BE = 2x$，高为$h$。
其面积为$\frac{(AD + CE)h}{2} = \frac{(2x + x)h}{2} = \frac{3xh}{2}$。
将$xh = 24$代入，得$\frac{3×24}{2} = 36cm^2$。
答案：B

11. 如图9所示,在正方形ABCD中,E为DC边上的点,连接BE,将$\triangle BCE$绕点C沿顺时针方向旋转$90^{\circ }得到\triangle DCF$,连接EF,若$∠BEC= 60^{\circ }$,则$∠EFD$的度数为(B)
A.$10^{\circ }$
B.$15^{\circ }$
C.$20^{\circ }$
D.$25^{\circ }$

答案： 解：
∵将△BCE绕点C顺时针旋转90°得到△DCF，
∴△BCE≌△DCF，∠ECF=90°，
∴CE=CF，∠BEC=∠DFC=60°，
∴△ECF为等腰直角三角形，∠CFE=45°，
∴∠EFD=∠DFC - ∠CFE=60° - 45°=15°．
答案：B

12. 分别画出图10中的图形绕点A顺时针旋转$90^{\circ }$、$180^{\circ }$、$270^{\circ }$后的图形.

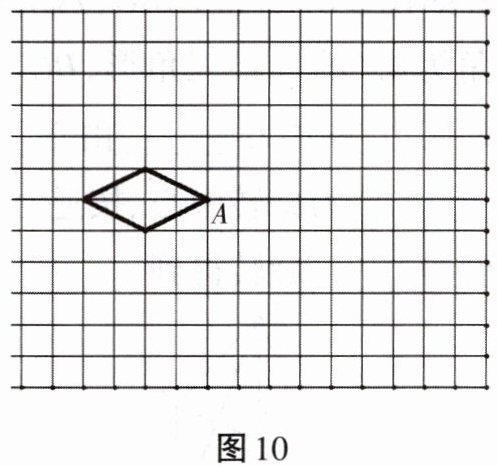
答案： 【解析】：
本题考查图形旋转，需要明确旋转中心、旋转方向和旋转角度，再根据这些要素确定旋转后图形各顶点的位置，最后依次连接各顶点得到旋转后的图形。
对于绕点$A$顺时针旋转$90^{\circ}$：
确定原图形各顶点绕点$A$顺时针旋转$90^{\circ}$后的位置。
以点$A$为旋转中心，将原图形的其他顶点分别绕点$A$顺时针旋转$90^{\circ}$，利用旋转的性质（旋转前后对应点到旋转中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角）来确定旋转后各顶点的坐标位置。
依次连接旋转后的各顶点，得到绕点$A$顺时针旋转$90^{\circ}$后的图形。
对于绕点$A$顺时针旋转$180^{\circ}$：
同样以点$A$为旋转中心，将原图形的各顶点绕点$A$顺时针旋转$180^{\circ}$。
此时，各顶点旋转后与原位置关于点$A$中心对称，根据中心对称的性质确定各顶点位置。
依次连接旋转后的各顶点，得到绕点$A$顺时针旋转$180^{\circ}$后的图形。
对于绕点$A$顺时针旋转$270^{\circ}$：
还是以点$A$为旋转中心，将原图形的各顶点绕点$A$顺时针旋转$270^{\circ}$。
可利用旋转性质或与旋转$90^{\circ}$的互补关系来确定各顶点位置。
依次连接旋转后的各顶点，得到绕点$A$顺时针旋转$270^{\circ}$后的图形。
【答案】：
图略（按照上述步骤分别画出绕点$A$顺时针旋转$90^{\circ}$、$180^{\circ}$、$270^{\circ}$后的图形即可）。

13. 如图11所示,四边形ABCD中,$∠BAD= ∠C= 90^{\circ }$,$AB= AD$,$AE⊥BC$于点E,$\triangle BEA旋转后能与\triangle DFA$重合.

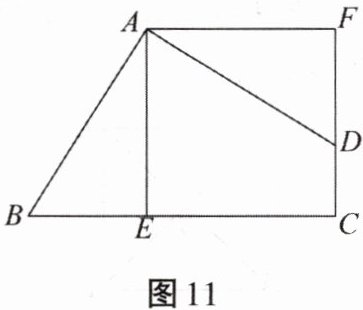
(1)旋转中心是哪一点？
(2)旋转了多少度？
(3)若$AE= 5cm$,求四边形AECF的面积.

答案：
(1)旋转中心是点A。
(2)旋转了90度。
(3)解：由旋转性质可知，△BEA≌△DFA，所以AE=AF，四边形AECF的面积=四边形AECD的面积+△DFA的面积=四边形AECD的面积+△BEA的面积=四边形ABCE的面积+四边形AECD的面积-△BEA的面积+△BEA的面积=四边形ABCF的面积。又因为AE⊥BC，∠C=90°，∠BAD=90°，AB=AD，可证四边形AECF为正方形，所以面积=AE²=5²=25cm²。
答：四边形AECF的面积为25cm²。