《2025年暑假作业八年级数学北师大版兰州大学出版社》

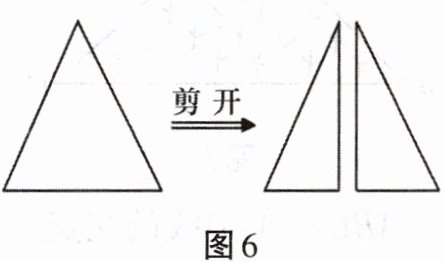
6. 如图6所示,有一腰长为5cm、底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有4个不同的四边形。

答案： 解：将两个全等直角三角形纸片拼四边形，可分以下情况：
1. 以直角边（2cm）为公共边拼接，有2种不同四边形；
2. 以直角边（√21cm）为公共边拼接，有2种不同四边形；
3. 以斜边（5cm）为公共边拼接，得到的是三角形，非四边形。
综上，共有4个不同的四边形。
答案：4

7. 如图7所示,在△ABC中,∠BAC＞90°,BC= 8,AB的中垂线交BC于点D,AC的中垂线交BC与点E,则△ADE的周长等于8。

答案： 解：
∵AB的中垂线交BC于点D，
∴AD=BD。
∵AC的中垂线交BC于点E，
∴AE=CE。
∵BC=8，
∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=8。
故答案为8。

8. 如图8所示,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB= AC= AD,有如下四个结论：①AC⊥BD；②BC= DE；③∠DBC= ∠BDC；④△ABC是正三角形。请写出正确结论的序号①③(把你认为正确结论的序号都填上)。

答案： ①③

9. 如图9所示,△ABC的周长为19cm,AC的垂直平分线DE交BC于点D,E为垂足,AE= 3cm,则△ABD的周长为13cm。

答案： 解：
∵DE是AC的垂直平分线，AE=3cm，
∴AD=DC，AC=2AE=6cm。
∵△ABC的周长为19cm，
∴AB+BC+AC=19cm，即AB+BD+DC+AC=19cm。
∵AD=DC，
∴AB+BD+AD+6=19cm，
∴AB+BD+AD=13cm，即△ABD的周长为13cm。
13

10. 在△ABC中,∠A= 50°,AB= AC,AB的垂直平分线DE交AC于点D,则∠DBC的度数是15°。

答案： 解：
∵在△ABC中，∠A=50°，AB=AC，
∴∠ABC=∠ACB=(180°-50°)/2=65°.
∵DE是AB的垂直平分线，
∴AD=BD，
∴∠ABD=∠A=50°，
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
15

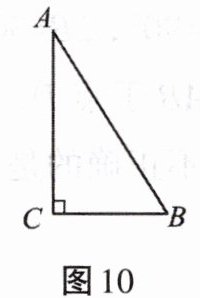
11. 如图10所示,在Rt△ABC中,∠C= 90°,∠A= 30°。
(1)尺规作图：作线段AB的垂直平分线l(保留作图痕迹,不写作法)；
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE。
求证：EF= 2DE。

答案：

(1) 直线 $l$ 即为所求.
(2) 证明: 在 $ \text{Rt} \triangle ABC $ 中, $ \angle A = 30^{\circ} $, $ \therefore \angle ABC = 60^{\circ} $. $ \because l $ 垂直平分 $ AB $, $ \therefore EA = EB $, $ \angle F = 30^{\circ} $, $ \therefore \angle EBA = \angle A = 30^{\circ} $, $ \therefore \angle EBC = 30^{\circ} $ 且在 $ \text{Rt} \triangle BED $ 中, $ EB = 2DE $, $ \because \angle F = 30^{\circ} = \angle EBC $, $ \therefore EF = EB = 2DE $.