《2025年暑假作业八年级数学北师大版兰州大学出版社》

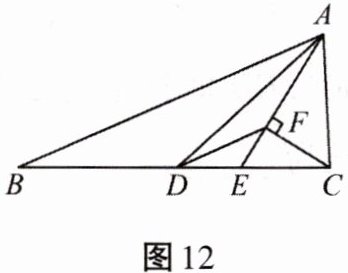
15. 如图12所示,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB= 5,AC= 2,则DF的长为多少？

答案：
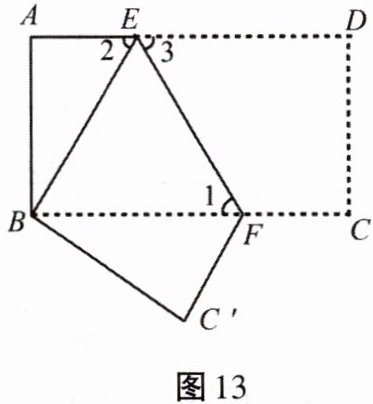
解析: 如图, 延长 CF 交 AB 于点 M, 由 AE 是角平分线, $ CF \perp AE $ 于点 F, 可以得出 $ \triangle ACF \cong \triangle AMF $, $ \therefore AC = AM = 2 $, $CF = MF $. 在 $ \triangle CBM $ 中, $ \because BD = CD $, $ \therefore DF $ 是 $ \triangle CBM $ 的中位线, $ \therefore DF = \frac { 1 } { 2 } BM = \frac { 1 } { 2 } ( A B - A M ) = \frac { 1 } { 2 } × 3 = 1.5 $.

16. 已知：如图13所示,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上.若∠1= 60°,AE= 1.
(1)求∠2、∠3的度数；
(2)求长方形纸片ABCD的面积S.

答案：
(1) 解：因为AD//BC，所以∠1=∠3=60°。由折叠性质得∠2=∠3=60°。
(2) 解：在Rt△ABE中，∠2=60°，AE=1，∠A=90°，所以∠ABE=30°，则BE=2AE=2，AB=$\sqrt{BE^2 - AE^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$。由折叠性质得DE=BE=2，所以AD=AE + DE=1 + 2=3。长方形ABCD面积S=AB×AD=$\sqrt{3}×3=3\sqrt{3}$。

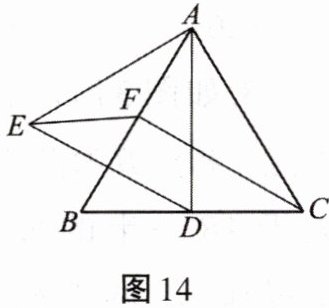
17. 如图14所示,△ABC是等边三角形,D、F分别是BC、AB上的点,且CD= BF,以AD为边作等边三角形ADE.
(1)求证：△ACD≌△CBF；
(2)点D在线段BC的何处时,四边形CDEF是平行四边形,且∠DEF= 30°？证明你的结论.

答案：
(1) 证明：
∵△ABC是等边三角形，
∴AC=CB，∠ACD=∠CBF=60°。
在△ACD和△CBF中，
$\left\{\begin{array}{l} AC=CB \\ \angle ACD=\angle CBF \\ CD=BF \end{array}\right.$
∴△ACD≌△CBF(SAS)。
(2) 当D是BC的中点时，四边形CDEF是平行四边形，且∠DEF=30°。
证明：
∵D是BC的中点，△ABC是等边三角形，
∴AD⊥BC，∠CAD=30°。
由
(1)知△ACD≌△CBF，
∴AD=CF，∠BCF=∠CAD=30°。
∵△ADE是等边三角形，
∴AD=DE，∠ADE=60°。
∴DE=CF，∠BDE=90°-∠ADE=30°。
∵∠BDE=∠BCF=30°，
∴DE//CF。
∵DE=CF且DE//CF，
∴四边形CDEF是平行四边形。
∴EF//BC，
∴∠DEF=∠BDE=30°。