《2025年暑假作业八年级数学北师大版兰州大学出版社》

8. 如图6所示,在Rt△ABC中,∠C= 90°,∠CAB= 60°,AD平分∠CAB,点D到AB的距离DE= 3.8cm,则线段BC的长为(C)
A.3.8cm
B.7.6cm
C.11.4cm
D.11.2cm

答案： 解：
∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DC=DE=3.8cm（角平分线性质）。
在Rt△ABC中，∠C=90°，∠CAB=60°，
∴∠B=30°。
在Rt△BDE中，∠B=30°，DE=3.8cm，
∴BD=2DE=7.6cm（30°角所对直角边是斜边一半）。
∴BC=BD+DC=7.6+3.8=11.4cm。
答案：C

9. 如图7所示,在平面直角坐标系中,点A(2,1)在第一象限,点P在x轴上,若以P、O、A为顶点的三角形是等腰三角形,则满足条件的点P共有(C)
A.2个
B.3个
C.4个
D.5个

答案： 解：设点P坐标为(x,0)，O(0,0)，A(2,1)。
1. OA=OP：
OA=$\sqrt{2^2+1^2}=\sqrt{5}$，则OP=|x|=$\sqrt{5}$，
解得$x=\sqrt{5}$或$x=-\sqrt{5}$，
点P为$(\sqrt{5},0)$，$(-\sqrt{5},0)$。
2. OA=AP：
OA=$\sqrt{5}$，AP=$\sqrt{(x-2)^2+(0-1)^2}=\sqrt{5}$，
即$(x-2)^2+1=5$，解得$x=4$或$x=0$（与O重合，舍去），
点P为(4,0)。
3. OP=AP：
OP=|x|，AP=$\sqrt{(x-2)^2+1}$，
则$x^2=(x-2)^2+1$，解得$x=\frac{5}{4}$，
点P为$(\frac{5}{4},0)$。
综上，满足条件的点P有$(\sqrt{5},0)$，$(-\sqrt{5},0)$，(4,0)，$(\frac{5}{4},0)$，共4个。
答案：C

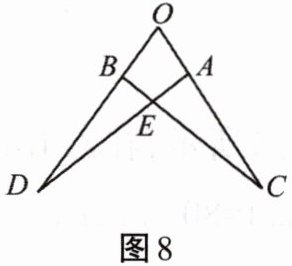
10. 如图8所示,若△OAD≌△OBC,且∠O= 65°,∠C= 20°,则∠OAD= ______.
95°

答案： 解：
∵△OAD≌△OBC，∠C=20°
∴∠D=∠C=20°
在△OAD中，∠O=65°，∠D=20°
∠OAD=180°-∠O-∠D=180°-65°-20°=95°
95°

11. 如图9所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、5、2、3,则最大的正方形E的面积是47.

答案： 解：设与正方形A、B相邻的直角三角形的斜边长为$m$，与正方形C、D相邻的直角三角形的斜边长为$n$，最大正方形E的边长为$k$。
因为所有三角形都是直角三角形，所有四边形都是正方形，根据勾股定理：
正方形A的面积为$3^2 = 9$，正方形B的面积为$5^2 = 25$，所以$m^2=9 + 25=34$；
正方形C的面积为$2^2 = 4$，正方形D的面积为$3^2 = 9$，所以$n^2=4 + 9=13$。
又因为最大正方形E的面积$k^2=m^2 + n^2$，所以$k^2=34+13=47$。
故最大正方形E的面积是$47$。

12. 等腰三角形的一个角是80°,则它的顶角是20°或80°.

答案： 解：
情况一：若80°角为顶角，则顶角为80°；
情况二：若80°角为底角，则顶角为180°-80°×2=20°。
综上，顶角是20°或80°。

13. 如图10所示,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是$28cm^2,AB= 20cm,AC= 8cm,DF= $2cm.

答案： 解：
∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC
∴DE=DF
设DF=DE=x cm
∵S△ABC=S△ABD+S△ACD=28 cm²
∴$\frac{1}{2} × AB × DE + \frac{1}{2} × AC × DF = 28$
即$\frac{1}{2} × 20x + \frac{1}{2} × 8x = 28$
10x + 4x = 28
14x = 28
x = 2
∴DF=2 cm

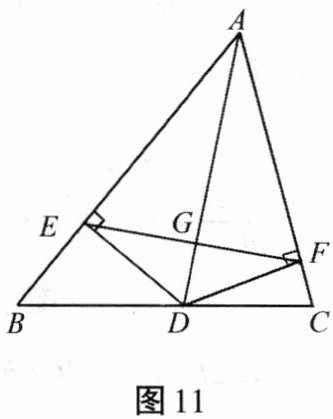
14. 如图11所示,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,判断AD与EF的位置关系.

答案： AD垂直平分EF。
证明：
∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF。
在Rt△AED和Rt△AFD中，
$\left\{\begin{array}{l} DE=DF\\ AD=AD\end{array}\right.$
∴Rt△AED≌Rt△AFD（HL），
∴AE=AF。
∵AE=AF，DE=DF，
∴AD垂直平分EF。