《2025年暑假作业八年级数学北师大版兰州大学出版社》

1. 在下列给出的五种运动中,其中属于平移的是(1), (4), (5).
(1)急刹车的小汽车在平直的公路上的向前滑行；(2)自行车轮子的运动；(3)时钟的分针的运动；(4)高层建筑内的电梯的运动；(5)左右推动推拉窗.

答案：
(1),
(4),
(5)

2. 将面积为$12cm^{2}$的等腰直角$\triangle ABC$向右上方平移20cm,得到$\triangle MNP$,则$\triangle MNP$是等腰直角三角形,它的面积是12$cm^{2}$.

答案： 等腰直角, 12

3. 如图1所示,四边形$ABCD$中,$AD// BC$,$BC = 8$,$AD = 3$,$AB = 4$,$CD = 3$,将$AB平移到DE$处,则$\triangle CDE$为直角三角形,周长为12.

答案： 解：
∵AD//BC，将AB平移到DE处，
∴四边形ABED是平行四边形，
∴BE=AD=3，DE=AB=4，
∵BC=8，
∴EC=BC-BE=8-3=5，
在△CDE中，DE=4，CD=3，EC=5，
∵3²+4²=5²，
∴△CDE为直角三角形，
周长为3+4+5=12。
直角，12

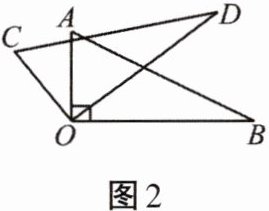
4. 如图2所示,$Rt\triangle AOB绕点O逆时针旋转到\triangle COD$的位置,若$\angle BOC = 127^{\circ}$,则旋转角度是____37°.

答案： 解：因为△AOB是直角三角形，所以∠AOB=90°。
由于Rt△AOB绕点O逆时针旋转到△COD的位置，所以旋转角为∠AOC或∠BOD。
已知∠BOC=127°，则∠AOC=∠BOC - ∠AOB=127° - 90°=37°。
故旋转角度是37°。

5. $\triangle ABC经过平移得到\triangle DEF$,并且点$A与D$,$B与E$,$C与F$是对应点,$AD = 3cm$,则$BE = $3$cm$,$AD与BE$之间的数量关系是相等,$AB与DE$之间的位置关系是平行或在同一条直线上.

答案： 3, 相等, 平行或在同一条直线上

6. 如图3所示,$\triangle ABC$中,$AC = 5$,中线$AD = 7$,$\triangle EDC是由\triangle ADB旋转180^{\circ}$所得,则$AB$边的取值范围是(D)
A.$1 ＜ AB ＜ 29$
B.$4 ＜ AB ＜ 24$
C.$5 ＜ AB ＜ 19$
D.$9 ＜ AB ＜ 19$

答案： 解：
∵△EDC是由△ADB旋转180°所得，
∴AB=EC，AD=ED=7，
∴AE=AD+ED=14。
在△AEC中，AC=5，AE=14，
根据三角形三边关系：AE-AC＜EC＜AE+AC，
即14-5＜EC＜14+5，
∴9＜EC＜19，
∵AB=EC，
∴9＜AB＜19。
答案：D

7. 下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转$120^{\circ}$后,能与原图形完全重合的是(A)

答案： 解：一个图形绕旋转中心顺时针旋转一定角度后能与原图形重合，则该角度为图形旋转对称角度。
- 选项A：图形被平均分成3份，旋转对称角度为$360^{\circ}÷3 = 120^{\circ}$，顺时针旋转$120^{\circ}$后能与原图形重合。
- 选项B：图形被平均分成4份，旋转对称角度为$360^{\circ}÷4 = 90^{\circ}$，顺时针旋转$120^{\circ}$后不能与原图形重合。
- 选项C：图形为中心对称图形，最小旋转对称角度为$180^{\circ}$，顺时针旋转$120^{\circ}$后不能与原图形重合。
- 选项D：图形被平均分成5份，旋转对称角度为$360^{\circ}÷5 = 72^{\circ}$，顺时针旋转$120^{\circ}$后不能与原图形重合。
结论：A

8. 剪纸文化是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是(A)

答案： A选项图案：沿某条直线折叠后直线两旁的部分能够完全重合，是轴对称图形；绕某一点旋转180°后能与自身重合，是中心对称图形。
B选项图案：是轴对称图形，但不是中心对称图形。
C选项图案：是轴对称图形，但不是中心对称图形。
D选项图案：既不是轴对称图形，也不是中心对称图形。
答案：A

9. 下列说法正确的是(B)
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移、旋转前后的图形全等
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到

答案： B