9. 如图9所示,在Rt△ABC中,∠C= 90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD= 3,AB= 10,则△ABD的面积是
15
.
答案:
解:由题意得,AP是∠BAC的平分线。
过点D作DE⊥AB于点E。
因为∠C=90°,所以DC⊥AC。
又因为AP平分∠BAC,CD=3,所以DE=CD=3。
△ABD的面积为$\frac{1}{2}×AB×DE=\frac{1}{2}×10×3=15$。
15
过点D作DE⊥AB于点E。
因为∠C=90°,所以DC⊥AC。
又因为AP平分∠BAC,CD=3,所以DE=CD=3。
△ABD的面积为$\frac{1}{2}×AB×DE=\frac{1}{2}×10×3=15$。
15
10. 如图10所示,AB= AC,∠BAC= 120°,AB的垂直平分线交BC于点D,那么∠ADC=
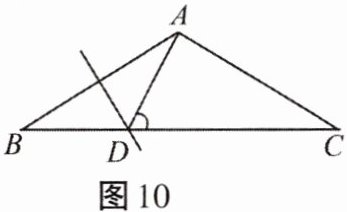
60°
.
答案:
解:连接AD。
∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-120°)/2=30°。
∵AB的垂直平分线交BC于D,
∴AD=BD,∠BAD=∠B=30°。
∴∠ADC=∠B+∠BAD=30°+30°=60°。
答案:60°
∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-120°)/2=30°。
∵AB的垂直平分线交BC于D,
∴AD=BD,∠BAD=∠B=30°。
∴∠ADC=∠B+∠BAD=30°+30°=60°。
答案:60°
11. 如图11所示,△ABC中,AB= AC,∠A= 36°,AC的垂直平分线交AB于点E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE= 5,求BC的长.
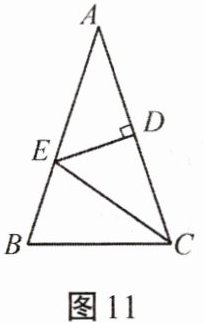
(1)求∠ECD的度数;
(2)若CE= 5,求BC的长.

(1) ∵ DE 垂直平分 AC,
∴ CE = AE,
∴ ∠ECD = ∠A = 36°;
(2) ∵ AB = AC,∠A = 36°,
∴ ∠B = ∠ACB = (180° - 36°)÷2 = 72°,
∵ ∠BEC = ∠A + ∠ECD = 36° + 36° = 72°,
∴ ∠BEC = ∠B,
∴ BC = EC = 5。
∴ CE = AE,
∴ ∠ECD = ∠A = 36°;
(2) ∵ AB = AC,∠A = 36°,
∴ ∠B = ∠ACB = (180° - 36°)÷2 = 72°,
∵ ∠BEC = ∠A + ∠ECD = 36° + 36° = 72°,
∴ ∠BEC = ∠B,
∴ BC = EC = 5。
答案:
(1)
∵ DE 垂直平分 AC,
∴ CE = AE,
∴ ∠ECD = ∠A = 36°;
(2)
∵ AB = AC,∠A = 36°,
∴ ∠B = ∠ACB = (180° - 36°)÷2 = 72°,
∵ ∠BEC = ∠A + ∠ECD = 36° + 36° = 72°,
∴ ∠BEC = ∠B,
∴ BC = EC = 5。
(1)
∵ DE 垂直平分 AC,
∴ CE = AE,
∴ ∠ECD = ∠A = 36°;
(2)
∵ AB = AC,∠A = 36°,
∴ ∠B = ∠ACB = (180° - 36°)÷2 = 72°,
∵ ∠BEC = ∠A + ∠ECD = 36° + 36° = 72°,
∴ ∠BEC = ∠B,
∴ BC = EC = 5。
12. 如图12所示,在Rt△ABC中,∠C= 90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,求∠B的度数.
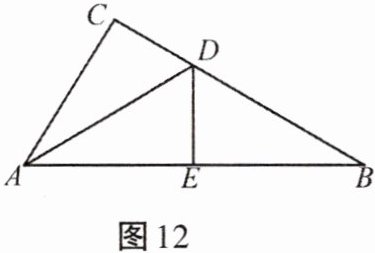

答案:
解:
∵DE垂直平分AB,
∴∠DAE=∠B。
∵在Rt△ABC中,∠C=90°,
∴∠CAB=90°-∠B。
∵AD平分∠CAB,
∴∠DAE=1/2∠CAB=1/2(90°-∠B)。
∵∠DAE=∠B,
∴1/2(90°-∠B)=∠B,
∴90°-∠B=2∠B,
∴3∠B=90°,
∴∠B=30°。
∵DE垂直平分AB,
∴∠DAE=∠B。
∵在Rt△ABC中,∠C=90°,
∴∠CAB=90°-∠B。
∵AD平分∠CAB,
∴∠DAE=1/2∠CAB=1/2(90°-∠B)。
∵∠DAE=∠B,
∴1/2(90°-∠B)=∠B,
∴90°-∠B=2∠B,
∴3∠B=90°,
∴∠B=30°。
查看更多完整答案,请扫码查看


