《2025年百年学典快乐假期暑假作业八年级综合北师大版》

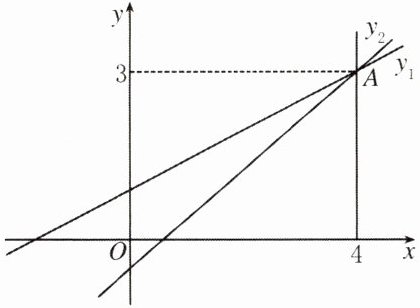
13. 如下图所示，一次函数 $ y_1 = kx + 1 $ 与 $ y_2 = mx - 1 $ 相交于点 $ A(4,3) $，当 $ y_2 ＜ y_1 $ 时，$ x $ 的取值范围是$x＜4$。

答案： $x＜4$

14. 数学何老师网购了一本《魔法数学》，同学们想知道书的价格，何老师让他们猜。甲说：“至少 $ 15 $ 元。”乙说：“至多 $ 25 $ 元。”丙说：“至多 $ 20 $ 元。”何老师说：“你们三个人中只有一人说对了”。则这本书的价格 $ x $（元）所在的范围为$x\gt25$。

答案： $x\gt25$

15. 某工程队进行爆破时，为了安全，人要撤离到距爆破点 $ 50m $ 以外的安全区域。已知引线的燃烧速度为 $ 0.2m/s $，爆破者离开速度为 $ 3m/s $，点燃时引线向远离爆破点的方向拉直，则引线的长度应满足什么条件？设引线长为 $ xm $，请根据题意列出关于 $ x $ 的不等式：$\frac{x}{0.2}＞\frac{50}{3}$。

答案： $\frac{x}{0.2}＞\frac{50}{3}$

16. 解不等式组 $ \begin{cases}3(x + 1) ＞ 5x + 4, & ① \\ \frac{x - 1}{2} \leq \frac{2x - 1}{3}, & ②\end{cases} $ 并将解集在数轴上表示出来。

答案： 【解析】：
本题可分别求解不等式组中两个不等式的解集，再取它们的交集得到不等式组的解集，最后将解集在数轴上表示出来。
- **步骤一：求解不等式$①$ $3(x + 1) \gt 5x + 4$。**
根据乘法分配律去括号可得：$3x + 3 \gt 5x + 4$。
移项：将含有$x$的项移到一边，常数项移到另一边，得到$3x - 5x \gt 4 - 3$。
合并同类项：计算可得$-2x \gt 1$。
系数化为$1$：不等式两边同时除以$-2$，根据不等式的性质，不等式两边同时除以一个负数，不等号方向改变，所以$x \lt -\frac{1}{2}$。
- **步骤二：求解不等式$②$ $\frac{x - 1}{2} \leq \frac{2x - 1}{3}$。**
去分母：不等式两边同时乘以$6$（$2$和$3$的最小公倍数），得到$6\times\frac{x - 1}{2} \leq 6\times\frac{2x - 1}{3}$，即$3(x - 1) \leq 2(2x - 1)$。
去括号：根据乘法分配律可得$3x - 3 \leq 4x - 2$。
移项：将含有$x$的项移到一边，常数项移到另一边，得到$3x - 4x \leq -2 + 3$。
合并同类项：计算可得$-x \leq 1$。
系数化为$1$：不等式两边同时除以$-1$，根据不等式的性质，不等式两边同时除以一个负数，不等号方向改变，所以$x \geq -1$。
- **步骤三：求不等式组的解集。**
综合不等式$①$的解集$x \lt -\frac{1}{2}$和不等式$②$的解集$x \geq -1$，取它们的交集，可得不等式组的解集为$-1 \leq x \lt -\frac{1}{2}$。
- **步骤四：在数轴上表示解集。**
在数轴上找到$-1$和$-\frac{1}{2}$对应的点，因为$x \geq -1$，所以在$-1$处用实心圆点表示；因为$x \lt -\frac{1}{2}$，所以在$-\frac{1}{2}$处用空心圆圈表示，然后在这两个点之间画线段表示解集。
【答案】：$-1 \leq x \lt -\frac{1}{2}$，数轴表示：先画数轴，找到$-1$和$-\frac{1}{2}$对应的点，在$-1$处标实心圆点，在$-\frac{1}{2}$处标空心圆圈，然后连接两点间的线段。

17. 开学初，小方和小亮去商店购买学习用品，小方用 $ 18 $ 元钱买了 $ 1 $ 支钢笔和 $ 3 $ 本笔记本，小亮用 $ 31 $ 元钱买了同样的钢笔 $ 2 $ 支和笔记本 $ 5 $ 本。
（1）求每支钢笔和每本笔记本的价格；
（2）校运会后，班主任拿出 $ 200 $ 元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共 $ 48 $ 件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出。

答案： 【解析】：
（1）设每支钢笔$x$元，每本笔记本$y$元。
根据小方用$18$元钱买了$1$支钢笔和$3$本笔记本，小亮用$31$元钱买了同样的钢笔$2$支和笔记本$5$本，可列方程组：
$\begin{cases}x + 3y = 18 \\2x + 5y = 31\end{cases}$
由第一个方程$x + 3y = 18$可得$x=18 - 3y$，将其代入第二个方程$2x + 5y = 31$中：
$2(18 - 3y)+5y = 31$
去括号得：$36-6y + 5y = 31$
合并同类项得：$36 - y = 31$
移项得：$y = 36 - 31$
解得：$y = 5$
把$y = 5$代入$x = 18 - 3y$得：$x=18-3×5=18 - 15 = 3$
所以每支钢笔$3$元，每本笔记本$5$元。
（2）设买钢笔$m$支，则买笔记本$(48 - m)$本。
根据班主任拿出$200$元购买奖品，可得$3m + 5(48 - m)\leq200$；
又因为笔记本数不少于钢笔数，所以$48 - m\geq m$。
解不等式$3m + 5(48 - m)\leq200$：
去括号得：$3m+240 - 5m\leq200$
移项得：$3m - 5m\leq200 - 240$
合并同类项得：$-2m\leq - 40$
两边同时除以$-2$，不等号变向得：$m\geq20$。
解不等式$48 - m\geq m$：
移项得：$48\geq m + m$
合并同类项得：$2m\leq48$
两边同时除以$2$得：$m\leq24$。
所以$m$的取值范围是$20\leq m\leq24$。
因为$m$为正整数，所以$m$的值为$20$、$21$、$22$、$23$、$24$。
当$m = 20$时，$48 - m = 48 - 20 = 28$；
当$m = 21$时，$48 - m = 48 - 21 = 27$；
当$m = 22$时，$48 - m = 48 - 22 = 26$；
当$m = 23$时，$48 - m = 48 - 23 = 25$；
当$m = 24$时，$48 - m = 48 - 24 = 24$。
故共有$5$种购买方案，分别为：
方案一：钢笔$20$支，笔记本$28$本；
方案二：钢笔$21$支，笔记本$27$本；
方案三：钢笔$22$支，笔记本$26$本；
方案四：钢笔$23$支，笔记本$25$本；
方案五：钢笔$24$支，笔记本$24$本。
【答案】：（1）每支钢笔$3$元，每本笔记本$5$元；（2）共有$5$种购买方案，分别为：方案一：钢笔$20$支，笔记本$28$本；方案二：钢笔$21$支，笔记本$27$本；方案三：钢笔$22$支，笔记本$26$本；方案四：钢笔$23$支，笔记本$25$本；方案五：钢笔$24$支，笔记本$24$本。

18. 已知不等式组 $ \begin{cases}x - 3(x - 2) \leq 4, \\ \frac{a + 2x}{3} ＞ x - 1\end{cases} $ 的解集为 $ 1 \leq x ＜ 2 $，求 $ a $ 的值。

答案： 【解析】：
本题可先分别求解不等式组中的两个不等式，再根据已知的解集求出$a$的值。
- **步骤一：解不等式$x - 3(x - 2) \leq 4$。**
去括号：根据乘法分配律$a(b - c)=ab - ac$，可得$x - 3x + 6 \leq 4$。
移项：将常数项$6$移到不等式右边，变为$x - 3x \leq 4 - 6$。
合并同类项：计算可得$-2x \leq -2$。
系数化为$1$：不等式两边同时除以$-2$，根据不等式的性质，不等式两边同时除以一个负数，不等号方向改变，可得$x \geq 1$。
- **步骤二：解不等式$\frac{a + 2x}{3} ＞ x - 1$。**
去分母：不等式两边同时乘以$3$，得到$a + 2x ＞ 3(x - 1)$。
去括号：根据乘法分配律可得$a + 2x ＞ 3x - 3$。
移项：将含$x$的项移到一边，常数项移到另一边，得到$2x - 3x ＞ -3 - a$。
合并同类项：计算可得$-x ＞ -3 - a$。
系数化为$1$：不等式两边同时除以$-1$，根据不等式的性质，不等式两边同时除以一个负数，不等号方向改变，可得$x ＜ 3 + a$。
- **步骤三：确定不等式组的解集。**
由步骤一可知$x \geq 1$，由步骤二可知$x ＜ 3 + a$，所以不等式组的解集为$1 \leq x ＜ 3 + a$。
- **步骤四：根据已知解集求$a$的值。**
已知不等式组的解集为$1 \leq x ＜ 2$，结合步骤三得到的解集$1 \leq x ＜ 3 + a$，可得$3 + a = 2$。
解方程$3 + a = 2$，移项可得$a = 2 - 3 = -1$。
【答案】：$-1$

19. 如右下图所示，有一高度为 $ 20cm $ 的容器，在容器中倒入 $ 100cm^3 $ 的水，此时刻度显示为 $ 5cm $，现将大小规格不同的两种玻璃球放入容器内，观察容器的体积变化测量玻璃球的体积。若每放入一个大玻璃球水面就上升 $ 0.5cm $。
（1）求一个大玻璃球的体积；
（2）放入 $ 27 $ 个大玻璃球后，开始放入小玻璃球，若放入 $ 5 $ 颗，水面没有溢出，再放入一颗，水面会溢出容器，求一个小玻璃球体积的范围。
（1）一个大玻璃球的体积是$10\,\text{cm}^3$；
（2）一个小玻璃球体积的范围是$5\,\text{cm}^3\lt V_{\text{小}}\leq6\,\text{cm}^3$。

答案： 【解析】：
（1）求一个大玻璃球的体积
已知倒入$100cm^3$的水，水面高度为$5cm$，根据长方体体积公式$V = S\times h$（$V$是体积，$S$是底面积，$h$是高），可得容器底面积$S=\frac{V}{h}=\frac{100}{5}=20cm^2$。
每放入一个大玻璃球水面上升$0.5cm$，根据上述公式，大玻璃球体积等于上升的水的体积，即$V_{大}=S\times\Delta h = 20\times0.5 = 10cm^3$。
 （2）求一个小玻璃球体积的范围
**计算放入$27$个大玻璃球后水面的高度**：
放入$27$个大玻璃球，水面上升的高度$h_{升1}=27\times0.5 = 13.5cm$，加上原来水的高度$5cm$，此时水面高度$h_1=5 + 13.5=18.5cm$。
**计算放入小玻璃球后水面高度的范围**：
容器高度为$20cm$，放入$5$颗小玻璃球水面没有溢出，再放入$1$颗水面溢出。
设一个小玻璃球体积为$V_{小}$，放入$5$颗小玻璃球时，水面上升的高度$h_{升2}$满足$18.5 + \frac{5V_{小}}{20}\leq20$；放入$6$颗小玻璃球时，水面上升的高度$h_{升3}$满足$18.5+\frac{6V_{小}}{20}＞20$。
**解不等式$18.5 + \frac{5V_{小}}{20}\leq20$**：
$\frac{5V_{小}}{20}\leq20 - 18.5$，$\frac{5V_{小}}{20}\leq1.5$，$V_{小}\leq1.5\times4$，$V_{小}\leq6$。
**解不等式$18.5+\frac{6V_{小}}{20}＞20$**：
$\frac{6V_{小}}{20}＞20 - 18.5$，$\frac{6V_{小}}{20}＞1.5$，$V_{小}＞1.5\times\frac{20}{6}$，$V_{小}＞5$。
所以$5cm^3\lt V_{小}\leq6cm^3$。
【答案】：
（1）一个大玻璃球的体积是$\boldsymbol{10cm^3}$；
（2）一个小玻璃球体积的范围是$\boldsymbol{5cm^3\lt V_{小}\leq6cm^3}$。