《2025年实验班提优训练暑假衔接版五升六年级数学苏教版》

例 下表中有15个数,选出5个数,使它们的和等于30,能做到吗? 为什么?

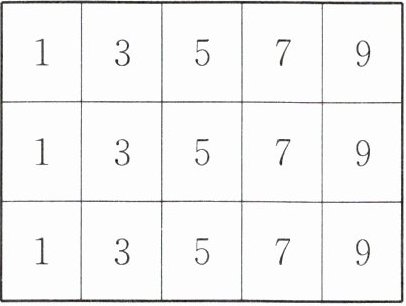
思路点拨 如果采用一个一个找、一个一个试、一个一个算的方法太麻烦了。最简单的方法是利用奇偶性来解决,因为奇数个奇数的和是奇数,表中15个数全是奇数,所以要找出5个数使它们的和为偶数是不可能的。

答案： 【解析】：根据奇数和偶数的性质，奇数个奇数相加的和为奇数。表中所有数均为奇数，选取5个奇数（奇数个），它们的和必然是奇数。而30是偶数，所以不可能做到。
【答案】：做不到。因为奇数个奇数的和是奇数，表中15个数全是奇数，从中任选5个数，它们的和仍是奇数，不可能是偶数，而30是偶数，所以做不到。

1. $1 + 2 + 3 + 4 + … + 2021$的和是奇数还是偶数?

答案： 加数中,偶数有 1010 个,它们的和是偶数;奇数有 1011 个,它们的和是奇数。因为偶数+奇数=奇数,所以和是奇数。

2. $2022 - 2021 + 2020 - 2019 + … + 2 - 1$的结果是奇数还是偶数?

答案： 因为$2022-2021=1$,$2020-2019=1$,$\cdots$,$2-1=1$,所以算式可以转化成$2022÷2=1011$(个)1 相加,它们的和是奇数,即结果是奇数。

3. $1 + 3 + 5 + 7 + … + 2021 + 2023$的和是奇数还是偶数?

答案： 算式里一共有 1012 个奇数相加,它们的和是偶数。

例 如果$a,b,c$是任意给定的三个整数,那么$(a + b)(b + c)(c + a)$的积是奇数还是偶数? 请说明理由。

答案： 思路点拨
(1)若$a,b,c$都是偶数,则两两之和也都是偶数,所以积是偶数。
(2)若$a,b,c$中有2个偶数、1个奇数,则两两之和中有1个偶数、2个奇数,所以积是偶数。
(3)若$a,b,c$中有1个偶数、2个奇数,则两两之和中有1个偶数、2个奇数,所以积是偶数。
(4)若$a,b,c$都是奇数,则两两之和都是偶数,所以积是偶数。
答案详解 因为$a,b,c$两两之和中至少有1个是偶数,偶数$×$整数= 偶数,所以积是偶数。