《2025年5年中考3年模拟九年级数学上册华师大版》

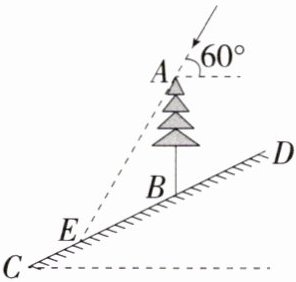
6. 「2024四川眉山中考,」如图,斜坡$CD的坡度i = 1:2$,在斜坡上有一棵垂直于水平面的大树$AB$,当太阳光与水平面的夹角为$60^{\circ}$时,大树在斜坡上的影子$BE的长为10$米,则大树$AB$的高为______米.

答案：
答案 $(4\sqrt{15}-2\sqrt{5})$
解析 如图，过点E作EH//CF，交AB的延长线于点H，则∠BEH = ∠DCF，
∴ tan∠BEH = tan∠DCF = $\frac{BH}{EH}=\frac{1}{2}$，设BH = x米，则EH = 2x米，
∴ BE = $\sqrt{EH^{2}+BH^{2}}=\sqrt{5}x$米，又
∵ BE = 10米，
∴ $\sqrt{5}x = 10$，解得x = $2\sqrt{5}$，
∴ BH = $2\sqrt{5}$米，EH = $4\sqrt{5}$米，
∵ ∠EAH = $180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}$，
∴ AH = $\sqrt{3}EH = 4\sqrt{15}$(米)，
∴ AB = AH - BH = $(4\sqrt{15}-2\sqrt{5})$米，即大树AB的高为$(4\sqrt{15}-2\sqrt{5})$米。

7. 跨物理力的分解「2024福建中考,」无动力帆船是借助风力前行的.如图所示的是帆船借助风力航行的平面示意图,已知帆船航行方向与风向所在直线的夹角$\angle PDA为70^{\circ}$,帆与航行方向的夹角$\angle PDQ为30^{\circ}$,风对帆的作用力$F为400N$.根据物理知识,$F可以分解为两个力F_1与F_2$,其中与帆平行的力$F_1$不起作用,与帆垂直的力$F_2又可以分解为两个力f_1与f_2$,$f_1$与航行方向垂直,被舵的阻力抵消,$f_2$与航行方向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大小,据此,建立数学模型：$F = AD = 400$,则

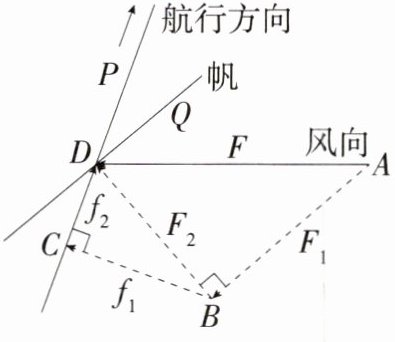
$f_2 = CD = $______128.(单位：$N$,参考数据：$\sin40^{\circ}\approx0.64$,$\cos40^{\circ}\approx0.77$)

答案： 答案 128
解析
∵ ∠PDA = $70^{\circ}$，∠PDQ = $30^{\circ}$，
∴ ∠ADQ = ∠PDA - ∠PDQ = $70^{\circ}-30^{\circ}=40^{\circ}$，
∵ AB//QD，
∴ ∠BAD = ∠ADQ = $40^{\circ}$，
∵ 在Rt△ABD中，F = AD = 400，∠ABD = $90^{\circ}$，
∴ F₂ = BD = AD·sin∠BAD = $400\cdot\sin40^{\circ}\approx400\times0.64 = 256$，由题意可知BD⊥DQ，
∴ ∠BDC = $180^{\circ}-90^{\circ}-\angle PDQ = 60^{\circ}$，
∵ 在Rt△BCD中，∠BCD = $90^{\circ}$，
∴ f₂ = CD = BD·cos∠BDC = $256\cdot\cos60^{\circ}=256\times\frac{1}{2}=128$。

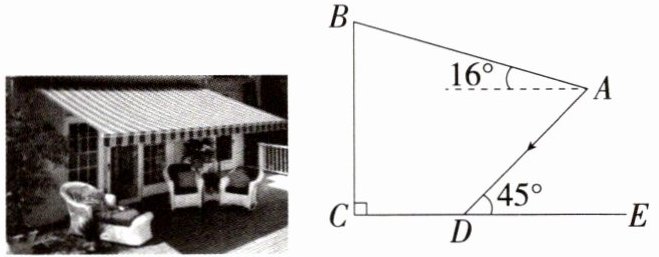
8. 「2024甘肃甘南州中考,」某校数学兴趣小组通过对如图所示的靠墙的遮阳篷进行实际测量,得到以下数据：遮阳篷$AB长为5m$,与水平面的夹角为$16^{\circ}$,且靠墙端离地高$BC为4m$,当太阳光线$AD与地面CE的夹角为45^{\circ}$时,求阴影$CD$的长.(参考数据：$\sin16^{\circ}\approx0.28$,$\cos16^{\circ}\approx0.96$,$\tan16^{\circ}\approx0.29$)

答案：
解析 如图，过点A作AG⊥BC于点G，作AF⊥CE于点F，则四边形AGCF是矩形，
∴ AG = CF，GC = AF，
∵ AB = 5m，∠BAG = $16^{\circ}$，
∴ AG = AB·cos∠BAG = $5\times\cos16^{\circ}\approx5\times0.96 = 4.8(m)$，BG = AB·sin∠BAG = $5\times\sin16^{\circ}\approx5\times0.28 = 1.4(m)$，
∴ CF = 4.8m，CG = 4 - 1.4 = 2.6(m)，
∴ AF = 2.6m，
∵ ∠ADF = $45^{\circ}$，
∴ DF = AF = 2.6m，
∴ CD = CF - DF = 4.8 - 2.6 = 2.2(m)。
故阴影CD的长约为2.2m。

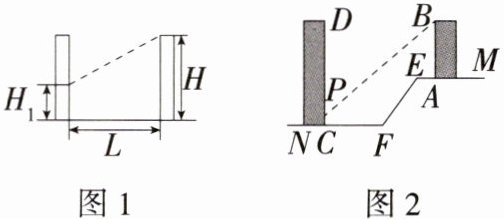
9. 新 课标应用意识“日照间距系数”反映了房屋日照情况.如图1,当前后房屋都朝向正南时,日照间距系数$= L:(H - H_1)$,其中$L$为楼间水平距离,$H$为南侧楼房高度,$H_1$为北侧楼房底层窗台至地面高度,如图2,山坡$EF$朝北,$EF长15m$,其坡度为$1:0.75$,山坡顶部平地$EM上有一高为24.3m的楼房AB$,底部$A到E点的距离为5m$.欲在$AB楼正北侧山脚的平地FN上建一楼房CD$,已知该楼底层窗台$P处至地面C处的高度为1.1m$,要使该楼的日照间距系数不低于$1.25$,底部$C距F$处至少多远？

答案：
解析 如图，过点E作EQ⊥NF，交NF的延长线于点Q，
∵ 山坡EF的坡度为1:0.75，
∴ $\frac{EQ}{FQ}=\frac{1}{0.75}=\frac{4}{3}$，
∴ 设EQ = 4x m，则FQ = 3x m，
∴ EF = $\sqrt{EQ^{2}+FQ^{2}}=5x$ m，
∵ EF = 15m，
∴ 5x = 15，解得x = 3，
∴ EQ = 4x = 12m，FQ = 3x = 9m，由题意得L = CF + FQ + EA = CF + 9 + 5 = CF + 14，H = AB + EQ = 24.3 + 12 = 36.3(m)，H₁ = 1.1m，
∴ 日照间距系数 = L:(H - H₁) = $\frac{CF+14}{36.3-1.1}=\frac{CF+14}{35.2}$，
∵ 该楼的日照间距系数不低于1.25，
∴ $\frac{CF+14}{35.2}\geq1.25$，
∴ CF ≥ 30m，
故要使该楼的日照间距系数不低于1.25，底部C距F处至少30m远。