《2025年5年中考3年模拟九年级数学上册华师大版》

1.「2025河南鹤壁淇滨联考」下列各式中,一定是二次根式的是(B)
A. $\sqrt {a^{2}-2}$
B. $\sqrt {a^{2}+3}$
C. $\sqrt [3]{8}$
D. $\sqrt {-2a}$

答案： B A、D 中被开方数均有可能是负数，所以 A、D 中的式子不一定是二次根式。C 中“$\sqrt[3]{}$”是三次根号，所以 C 中式子不是二次根式。B 中 $a^{2}+3＞0$，所以 $\sqrt{a^{2}+3}$一定是二次根式。

2. 若$\sqrt [|1-b|]{5b-7}$是二次根式,则b的值是2。

答案： 答案 2
解析 $\because \sqrt[|-b|]{5b - 7}$是二次根式，$\therefore |-b| = 2$，$5b - 7\geqslant0$，$\therefore b = 2$。

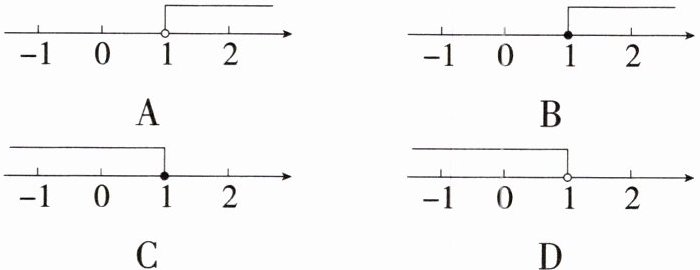
3.「2023内蒙古通辽中考」二次根式$\sqrt {1-x}$在实数范围内有意义,则实数x的取值范围在数轴上表示为(C)

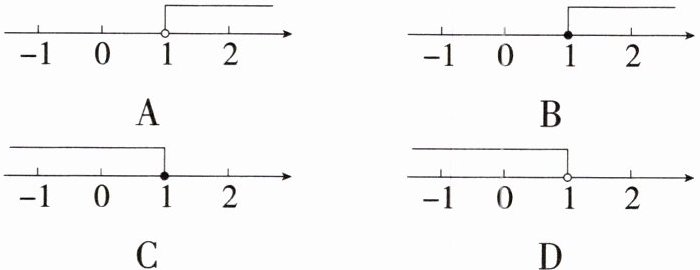
答案： C  

4. 新开放探究题「2023湖南永州中考」已知x为正整数,写出一个使$\sqrt {x-3}$在实数范围内没有意义的x的值：1。

答案： 答案 1（或 2）
解析 要使 $\sqrt{x - 3}$在实数范围内没有意义，则 $x - 3＜0$，$\therefore x＜3$，$\because x$ 为正整数，$\therefore x$ 的值是 1 或 2。

5.「2024河南新乡金龙学校月考」求使下列式子有意义的x的取值范围。
（1）$\sqrt{2-3x}$中x的取值范围是$x＜\frac{2}{3}$
（2）$\frac{1}{1-\sqrt{x}}$中x的取值范围是$x\geqslant0$且$x\neq1$
（3）$\frac{\sqrt{x+2}}{x-1}$中x的取值范围是$x＞-2$且$x\neq1$
（4）$\sqrt{x+2}+\sqrt{5-x}$中x的取值范围是$-2\leqslant x\leqslant5$

答案： 解析 （1）根据题意得 $2 - 3x＞0$，解得 $x＜\frac{2}{3}$。
（2）根据题意得 $x\geqslant0$ 且 $1 - \sqrt{x}\neq0$，解得 $x\geqslant0$ 且 $x\neq1$。
（3）根据题意得 $x + 2＞0$ 且 $x - 1\neq0$，解得 $x＞-2$ 且 $x\neq1$。
（4）由题意得 $\begin{cases}x + 2\geqslant0\\5 - x\geqslant0\end{cases}$，解得 $-2\leqslant x\leqslant5$。

6.「2025福建泉州培元中学月考」若$\sqrt {(x+3)^{2}}= 3+x$,则x的取值范围是(A)
A. $x≥-3$
B. $x≤-3$
C. $x＞3$
D. $x＜3$

答案： A $\because \sqrt{(x + 3)^{2}} = 3 + x$，$\therefore 3 + x\geqslant0$，$\therefore x\geqslant - 3$。

7. 学科教材变式特色P413「2024四川乐山中考」已知$1＜x＜2$,化简$\sqrt {(x-1)^{2}}+|x-2|$的结果为(B)
A. -1
B. 1
C. $2x-3$
D. $3-2x$

答案： B $\because 1＜x＜2$，$\therefore x - 1＞0$，$x - 2＜0$，$\therefore \sqrt{(x - 1)^{2}} + |x - 2| = x - 1 + 2 - x = 1$。

8. 已知x,y均为有理数,且满足$\sqrt {1+x}= (y-1)\cdot \sqrt {1-y}$,则$x^{2023}-y^{2023}= $-2。

答案： 答案 -2
解析 由题意知 $\sqrt{1 + x}\geqslant0$，$\sqrt{1 - y}\geqslant0$，$1 - y\geqslant0$，$\therefore (y - 1)\sqrt{1 - y}\leqslant0$，$\therefore 1 + x = 0$，$1 - y = 0$，$\therefore x = - 1$，$y = 1$，$\therefore x^{2023} - y^{2023} = (-1)^{2023} - 1^{2023} = - 2$。

9.「2025吉林长春第二外国语学校月考改编」计算：
(1)$\sqrt {(-\frac {2}{3})^{2}}=$$\frac{2}{3}$。
(2)$-\sqrt {(-6)^{2}}=$-6。
(3)$(\frac {5}{7}\sqrt {\frac {7}{5}})^{2}=$$\frac{5}{7}$。
(4)$\sqrt {9×10^{-2}}=$0.3。

答案： 答案 （1）$\frac{2}{3}$ （2）-6 （3）$\frac{5}{7}$ （4）0.3
解析 （1）原式 $=\left|-\frac{2}{3}\right|=\frac{2}{3}$。
（2）原式 $=-| - 6| = - 6$。
（3）原式 $=\left(\frac{5}{7}\right)^{2}\times\left(\sqrt{\frac{7}{5}}\right)^{2}=\frac{5}{7}\times\frac{5}{7}\times\frac{7}{5}=\frac{5}{7}$。
（4）原式 $=\sqrt{(3\times10^{-1})^{2}} = 3\times10^{-1} = 0.3$。

10.「2025海南海口美兰一模,★☆」若代数式$\sqrt {-a}+\frac {1}{\sqrt {ab}}$有意义,则点$(a,b)$在平面直角坐标系中的(C)
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： C 由题意可得 $-a\geqslant0$，$ab＞0$，$\therefore a＜0$，$b＜0$，$\therefore$ 点 $(a,b)$ 在第三象限。

11.「2025山西临汾实验中学校月考,★☆」已知a,b都是实数,若$\sqrt {2x+y}+(x-y+3)^{2}= 0$,则$(x+y)^{2025}$的值是(1)
A. 2025
B. -2025
C. 1
D. -1

答案： C $\because \sqrt{2x + y}\geqslant0$，$(x - y + 3)^{2}\geqslant0$，$\sqrt{2x + y} + (x - y + 3)^{2} = 0$，$\therefore 2x + y = 0$，$x - y + 3 = 0$，解得 $x = - 1$，$y = 2$，$\therefore (x + y)^{2025} = 1^{2025} = 1$。

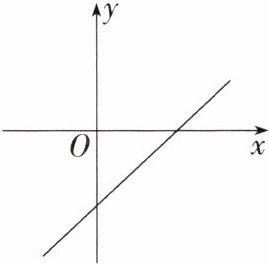
12.「2024河南洛阳第二外国语学校月考,★☆」直线$y= (m-3)x+n-2$(m,n是常数)如图所示,则化简$|m-n|+\sqrt {n^{2}-4n+4}$的结果为$m - 2n + 2$。

答案： 答案 $m - 2n + 2$
解析 由题图得 $\begin{cases}m - 3＞0\\n - 2＜0\end{cases}$，解得 $\begin{cases}m＞3\\n＜2\end{cases}$，$\therefore |m - n| + \sqrt{n^{2} - 4n + 4} = m - n + \sqrt{(n - 2)^{2}} = m - n + 2 - n = m - 2n + 2$。

13.「2025河南鹤壁淇县二模,★☆」若$\sqrt {(2024-a)^{2}}+\sqrt {a-2025}= a$,则$a-2024^{2}$的值是____2025。

答案： 答案 2025
解析 由题意得 $a - 2025\geqslant0$，$\therefore a\geqslant2025$，$\therefore 2024 - a＜0$，$\therefore \sqrt{(2024 - a)^{2}} + \sqrt{a - 2025} = a - 2024 + \sqrt{a - 2025} = a$，$\therefore \sqrt{a - 2025} = 2024$，$\therefore a - 2025 = 2024^{2}$，$\therefore a - 2024^{2} = 2025$。