第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.下列命题是真命题的是 (
A.锐角三角形都相似
B.钝角三角形都相似
C.相似的两个三角形不一定全等
D.全等的两个三角形不一定相似
C
)A.锐角三角形都相似
B.钝角三角形都相似
C.相似的两个三角形不一定全等
D.全等的两个三角形不一定相似
答案:
C 相似的两个三角形形状一定相同,但大小不一定相等,故二者不一定全等。
2.「2025 湖南师大附中梅溪湖中学月考」如图,如果$△ACP$$\backsim △ABC,∠A= 100^{\circ },∠B= 20^{\circ }$,那么$∠APC$的度数是____
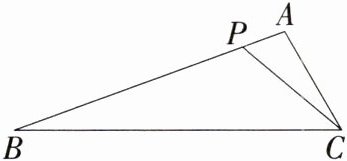
60°
.
答案:
答案 $60^{\circ}$
解析 $\because \angle A = 100^{\circ}, \angle B = 20^{\circ}, \therefore \angle ACB = 180^{\circ} - \angle A - \angle B = 60^{\circ}, \because \triangle ACP \backsim \triangle ABC, \therefore \angle APC = \angle ACB = 60^{\circ}$。
解析 $\because \angle A = 100^{\circ}, \angle B = 20^{\circ}, \therefore \angle ACB = 180^{\circ} - \angle A - \angle B = 60^{\circ}, \because \triangle ACP \backsim \triangle ABC, \therefore \angle APC = \angle ACB = 60^{\circ}$。
3.「2024 吉林长春第二实验中学月考」如图,三角尺在灯光照射下形成投影,三角尺与其投影的相似比为$2:5$,且三角尺的一边长为8 cm,则其投影三角尺的对应边长为 (
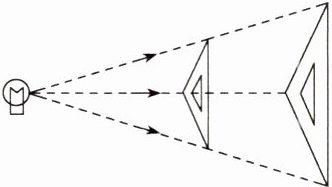
A.20 cm
B.10 cm
C.8 cm
D.3.2 cm
20
)
A.20 cm
B.10 cm
C.8 cm
D.3.2 cm
答案:
A 设其投影三角尺的对应边长为 $x$ cm,$\because$ 三角尺与其投影的相似比为 $2:5$,$\therefore 8:x = 2:5$,解得 $x = 20$。
4.「2025 北京通州一模」如图,$△ABC和△A_{1}B_{1}C_{1}均在4×4$的正方形网格(每个小正方形的边长都为1)中,$△ABC与△A_{1}B_{1}C_{1}$的顶点都在网格线的交点处.若$△ABC\backsim △A_{1}B_{1}C_{1}$,则它们的相似比是____

$\sqrt{2}:1$
.
答案:
答案 $\sqrt{2}:1$
解析 由网格可知 $AC = \sqrt{1^{2} + 1^{2}} = \sqrt{2}, A_{1}C_{1} = 1$,$\because \triangle ABC \backsim \triangle A_{1}B_{1}C_{1}, \frac{AC}{A_{1}C_{1}} = \frac{\sqrt{2}}{1} = \sqrt{2}, \therefore$ 相似比是 $\sqrt{2}:1$。
解析 由网格可知 $AC = \sqrt{1^{2} + 1^{2}} = \sqrt{2}, A_{1}C_{1} = 1$,$\because \triangle ABC \backsim \triangle A_{1}B_{1}C_{1}, \frac{AC}{A_{1}C_{1}} = \frac{\sqrt{2}}{1} = \sqrt{2}, \therefore$ 相似比是 $\sqrt{2}:1$。
5.「2024 甘肃天水秦州期中」如图,$AB// CD$,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有 (
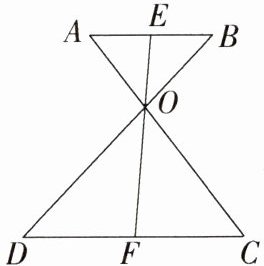
A.1对
B.2对
C.3对
D.4对
C
)
A.1对
B.2对
C.3对
D.4对
答案:
C $\because AB // CD, \therefore \triangle AEO \backsim \triangle CFO, \triangle BEO \backsim \triangle DFO, \triangle ABO \backsim \triangle CDO$,共 3 对。
6.「2024 河南中考」如图,在$□ ABCD$中,对角线AC,BD相交于点O,点E为OC的中点,$EF// AB$交BC于点F.若$AB= 4$,则EF的长为 (
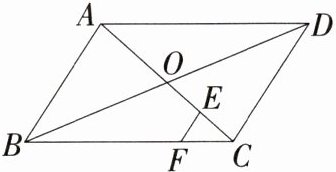
A.$\frac {1}{2}$
B.1
C.$\frac {4}{3}$
D.2
B
)
A.$\frac {1}{2}$
B.1
C.$\frac {4}{3}$
D.2
答案:
B $\because$ 四边形 $ABCD$ 是平行四边形,$\therefore OC = \frac{1}{2}AC$,$\because$ 点 $E$ 为 $OC$ 的中点,$\therefore CE = \frac{1}{2}OC = \frac{1}{4}AC$,$\because EF // AB$,$\therefore \triangle CEF \backsim \triangle CAB$,$\therefore \frac{EF}{AB} = \frac{CE}{AC}$,即 $\frac{EF}{4} = \frac{1}{4}$,$\therefore EF = 1$。
7.「2025 陕西师大附中月考」如图,在菱形ABCD中,点E在边AD上(不与点A,D重合),射线BE与射线CD交于点F,求证:$\frac {BE}{AB}= \frac {BF}{CF}$.
证明:
证明:
∵四边形ABCD是菱形,∴AB//CF,∴∠ABE=∠CFB,∠BAE=∠FDE,∴△ABE∽△DFE,∴$\frac{AB}{DF}=\frac{BE}{EF}$,∴$\frac{EF}{DF}=\frac{BE}{AB}$。∵AB//CF,∴∠F=∠ABE,∠FDE=∠A,∴△DEF∽△CBF,∴$\frac{EF}{BF}=\frac{DF}{CF}$,∴$\frac{EF}{DF}=\frac{BF}{CF}$,∴$\frac{BE}{AB}=\frac{BF}{CF}$
.
答案:
证明 $\because$ 四边形 $ABCD$ 是菱形,$\therefore AB // CF, DE // BC$,$\therefore \triangle ABE \backsim \triangle DFE$,$\therefore \frac{AB}{DF} = \frac{BE}{EF}$,$\therefore \frac{EF}{DF} = \frac{BE}{AB}$。$\because DE // BC$,$\therefore \triangle DEF \backsim \triangle CBF$,$\therefore \frac{EF}{BF} = \frac{DF}{CF}$,$\therefore \frac{EF}{DF} = \frac{BF}{CF}$,$\therefore \frac{BE}{AB} = \frac{BF}{CF}$。
查看更多完整答案,请扫码查看


