《2025年5年中考3年模拟九年级数学上册华师大版》

1.「2025 福建莆田城厢期中」如图,某“综合与实践”小组为测量河两岸 A,P 两点间的距离,在点 A 所在岸边的平地上取点 B、C、D,使 A、B、C 在同一条直线上,且 $ AC \perp AP $,使 $ CD \perp AC $,且 P、B、D 三点在同一条直线上.若测得 $ AB = 15 \, \text{m} $, $ BC = 3 \, \text{m} $, $ CD = 8 \, \text{m} $,则 A、P 两点间的距离为 (40m)

A. $ 60 \, \text{m} $
B. $ 40 \, \text{m} $
C. $ 30 \, \text{m} $
D. $ 20 \, \text{m} $

答案： B
∵AC⊥AP,CD⊥AC,
∴∠A=∠C=90°,
∵∠ABP=∠CBD,
∴△ABP∽△CBD,
∴$\frac{AB}{BC}$=$\frac{AP}{CD}$,
∵AB=15m,BC=3m,CD=8m,
∴$\frac{15}{3}$=$\frac{AP}{8}$,
∴AP=40m.

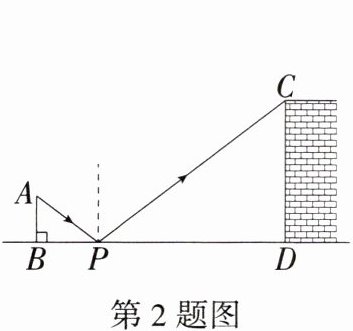
2.「2025 甘肃天水二模」如图所示的是一位同学用激光笔测量某古城墙高度的示意图.点 P 处水平放置一面平面镜,光线从点 A 出发经平面镜反射后刚好到古城墙 CD 的顶端 C 处,若 $ AB \perp BD $, $ CD \perp BD $,测得 $ AB = 1.5 \, \text{m} $, $ BP = 2 \, \text{m} $, $ PD = 6 \, \text{m} $,则该古城墙的高度 CD 是 (4.5m)

A. $ 3 \, \text{m} $
B. $ 4.5 \, \text{m} $
C. $ 8 \, \text{m} $
D. $ 5 \, \text{m} $

答案： B 由题意可知∠APB=∠CPD,
∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°,
∴△ABP∽△CDP,
∴$\frac{AB}{CD}$=$\frac{BP}{DP}$,
∴$\frac{1.5}{CD}$=$\frac{2}{6}$,
∴CD=4.5m,
∴该古城墙的高度CD是4.5m.

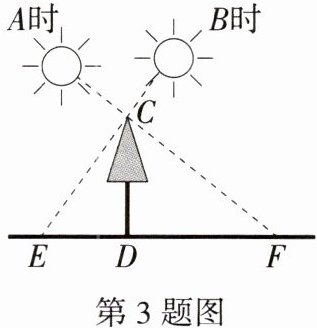
3.「2025 河南郑州金水期中」如图,嘉嘉在 A 时测得一棵 $ 4 \, \text{m} $ 高的树的影长 DF 为 $ 8 \, \text{m} $,若 A 时和 B 时两次日照的光线互相垂直,则 B 时这棵树的影长 DE 为 (2m)

A. $ 2 \, \text{m} $
B. $ 2 \sqrt { 5 } \, \text{m} $
C. $ 4 \, \text{m} $
D. $ 4 \sqrt { 2 } \, \text{m} $

答案： A 根据题意得CE⊥CF,
∴∠ECF=90°,
∴∠ECD+∠DCF=90°,
∵CD⊥EF,
∴∠CDE=∠CDF=90°,
∴∠CFD+∠DCF=90°,
∴∠ECD=∠CFD,
∴△CDE∽△FDC,
∴$\frac{ED}{CD}$=$\frac{CD}{FD}$,即CD²=ED·FD,
∵CD=4m,FD=8m,
∴4²=8ED,解得ED=2m,即B时这棵树的影长DE为2m.

4. 学科特色 教材变式 P74T1「2025 重庆巴蜀中学期中」如图,同一时刻在阳光照射下,树 AB 的影长 $ BC = 4.5 \, \text{m} $,小明的影长 $ B ^ { \prime } C ^ { \prime } = 1.5 \, \text{m} $,已知小明的身高 $ A ^ { \prime } B ^ { \prime } = 1.7 \, \text{m} $,则树高 $ AB = $5.1$ \text{m} $.

答案： 答案 5.1
解析 设树高为xm,
∵$\frac{\text{树高}}{\text{树的影长}}=\frac{\text{小明的身高}}{\text{小明的影长}}$,
∴$\frac{x}{4.5}$=$\frac{1.7}{1.5}$,
∴x=5.1,即树高为5.1m.

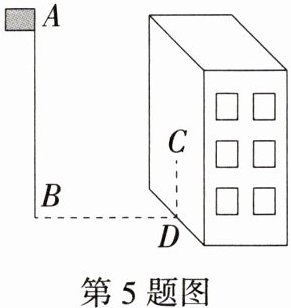
5.「2025 山西长治屯留期中」某同学想测量旗杆的高度,如图,他在某一时刻测得 1 米长的竹竿竖直放置时影长为 1.5 米,在同时刻测量旗杆的影长时,因旗杆靠近一教学楼,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为 21 米,落在墙上的影高为 2 米,则旗杆的高度为______米.

答案：
答案 16
解析 如图,过点C作CE⊥AB于点E,竹竿、竹竿的影子、光线构成的三角形为△FGH,此时FG=1米,GH=1.5米,BD=EC=21米,CD=EB=2米.易得△AEC∽△FGH,
∴$\frac{AE}{FG}$=$\frac{EC}{GH}$,
∴$\frac{AE}{1}$=$\frac{21}{1.5}$,
∴AE=14米,
∴AB=AE+BE=14+2=16(米).

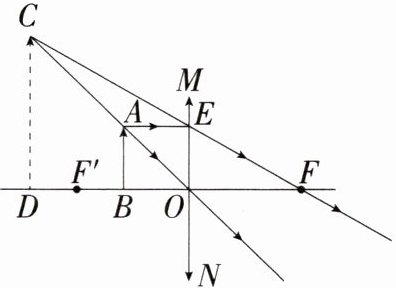
6. 跨物理 凸透镜成像「2025 福建漳州二模, ★☆」如图所示的是凸透镜成像示意图,CD 是蜡烛 AB 通过凸透镜 MN 所成的虚像.已知蜡烛的高 AB 为 $ 5.4 \, \text{cm} $,蜡烛 AB 离凸透镜 MN 的水平距离 OB 为 $ 6 \, \text{cm} $,该凸透镜的焦距 OF 为 $ 10 \, \text{cm} $, $ AE // OF $,则像 CD 的高为 (13.5cm)

A. $ 15 \, \text{cm} $
B. $ 14.4 \, \text{cm} $
C. $ 13.5 \, \text{cm} $
D. $ 9 \, \text{cm} $

答案： C 由题意得AB//MN,AE//OF,AB//CD,
∴四边形ABOE是平行四边形,
∴AE=OB=6cm,
∵AE//OF,
∴△CAE∽△COF,
∴$\frac{CA}{CO}$=$\frac{AE}{OF}$,
∴$\frac{CA}{CO}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴$\frac{OA}{CO}$=$\frac{2}{5}$,
∵AB//CD,
∴△OAB∽△OCD,
∴$\frac{AB}{CD}$=$\frac{OA}{CO}$,
∴$\frac{5.4}{CD}$=$\frac{2}{5}$,
∴CD=13.5cm.

7. 新考向 数学文化「2022 浙江衢州中考, ★☆」西周数学家商高总结了用“矩”(如图 1)测量物高的方法:把矩的两边放置成如图 2 所示的位置,从矩的一端 A(人眼)望点 E,使视线通过点 C,记人站立的位置为点 B,量出 BG 的长,即可算得物高 EG.令 $ BG = x ( \text{m} ) $, $ EG = y ( \text{m} ) $,若 $ a = 30 \, \text{cm} $, $ b = 60 \, \text{cm} $, $ AB = 1.6 \, \text{m} $,则 y 关于 x 的函数表达式为($y=\frac{1}{2}x+1.6$)
A. $ y = \frac { 1 } { 2 } x $
B. $ y = \frac { 1 } { 2 } x + 1.6 $
C. $ y = 2 x + 1.6 $
D. $ y = \frac { 1800 } { x } + 1.6 $

答案： B 由题图可得AF=BG=xm,EF=EG−FG,FG=AB=1.6m,
∵EG=ym,
∴EF=(y−1.6)m,
∵EG=ym,
∴EF=(y−1.6)m,
∵CD⊥AF,EF⊥AF,
∴CD//EF,
∴△ADC∽△AFE,
∴$\frac{CD}{EF}$=$\frac{AD}{AF}$,即$\frac{30}{EF}$=$\frac{60}{AF}$,
∴$\frac{30}{y−1.6}$=$\frac{60}{x}$,化简得$y=\frac{1}{2}x+1.6$.