《2025年5年中考3年模拟九年级数学上册华师大版》

8. 「2023 湖南常德中考」如图 1,在$Rt\triangle ABC$中,$∠ABC = 90^{\circ}$,$AB = 8$,$BC = 6$,D 是 AB 上一点,且$AD = 2$,过点 D 作$DE // BC$交 AC 于 E,将$\triangle ADE$绕 A 点顺时针旋转到图 2 所示的位置. 则图 2 中$\frac {BD}{CE}$的值为______$\frac{4}{5}$.

答案： 答案　$\frac{4}{5}$
解析
∵∠ABC=90°，AB=8，BC=6，
∴AC=$\sqrt{AB^{2}+BC^{2}}$=$\sqrt{8^{2}+6^{2}}$=10。在题图1中，
∵DE//BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$，即$\frac{AD}{AE}$=$\frac{AB}{AC}$。
∵将△ADE绕A点顺时针旋转到题图2所示的位置，
∴∠DAB=∠EAC，
∴△ADB∽△AEC，
∴$\frac{BD}{CE}$=$\frac{AB}{AC}$=$\frac{8}{10}$=$\frac{4}{5}$。

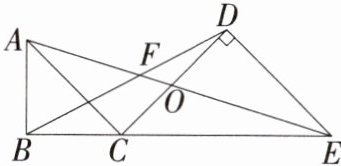
9. 「2025 甘肃天水秦安一模」如图,$\triangle ABC和\triangle CDE$都是等腰直角三角形,$∠ABC和∠CDE$是直角,B、C、E 三点共线,连结 AE 和 BD,相交于点 F,AE 交 CD 于点 O. 求证:
(1)$\triangle BCD \backsim \triangle ACE$.
证明：∵△ABC和△CDE都是等腰直角三角形，∴$\frac{AC}{BC}$=$\frac{CE}{CD}$=$\sqrt{2}$，∠ACB=∠DCE=45°，
∴∠ACB+∠ACD=∠DCE+∠ACD，
即∠BCD=∠ACE，∴△BCD∽△ACE。
(2)$OC^{2} = OA \cdot OF$.
证明：∵△BCD∽△ACE，∴∠BDC=∠AEC，
∵∠COE=∠FOD，∴△COE∽△FOD，∴$\frac{OC}{OF}$=$\frac{OE}{OD}$①，
∵∠ACB=∠DCE=45°，∴∠ACD=∠CDE=90°，
∴AC//DE，∴$\frac{OC}{OD}$=$\frac{OA}{OE}$②，
①×②，得$\frac{OC}{OF}\cdot\frac{OC}{OD}=\frac{OE}{OD}\cdot\frac{OA}{OE}$，∴$OC^{2}=OA\cdot OF$。

答案： 证明　
(1)
∵△ABC和△CDE都是等腰直角三角形，
∴$\frac{AC}{BC}$=$\frac{CE}{CD}$=$\sqrt{2}$，∠ACB=∠DCE=45°，
∴∠ACB+∠ACD=∠DCE+∠ACD，
即∠BCD=∠ACE，
∴△BCD∽△ACE。
(2)
∵△BCD∽△ACE，
∴∠BDC=∠AEC，
∵∠COE=∠FOD，
∴△COE∽△FOD，
∴$\frac{OC}{OF}=\frac{OE}{OD}$①，
∵∠ACB=∠DCE=45°，
∴∠ACD=∠CDE=90°，
∴AC//DE，
∴$\frac{OC}{OD}=\frac{OA}{OE}$②，
①×②，得$\frac{OC}{OF}\cdot\frac{OC}{OD}=\frac{OE}{OD}\cdot\frac{OA}{OE}$，
∴$OC^{2}=OA\cdot OF$。

10. 新课标推理能力「2024 四川乐山沐川模拟」如图,已知$∠MON = 90^{\circ}$,A 是$∠MON$内部的一点,过点 A 作$AB ⊥ ON$,垂足为点 B,$AB = 3cm$,$OB = 4cm$,动点 E,F 同时从 O 点出发,点 E 以$1.5cm/s$的速度沿 ON 方向运动,点 F 以$2cm/s$的速度沿 OM 方向运动,EF 与 OA 交于点 C,连结 AE,当点 E 到达点 B 时停止运动,点 F 随之停止运动. 设运动时间为$t s(t ＞ 0)$.
(1)当$t = 1$时,$\triangle EOF与\triangle ABO$是否相似? 请说明理由.当t=1时，△EOF与△ABO相似，理由如下：∵t=1，∴OE=1.5cm，OF=2cm，∵AB=3cm，OB=4cm，∴$\frac{OE}{AB}$=$\frac{1.5}{3}$=$\frac{1}{2}$，$\frac{OF}{BO}$=$\frac{2}{4}$=$\frac{1}{2}$，∴$\frac{OE}{AB}$=$\frac{OF}{OB}$，∵∠EOF=∠ABO=90°，∴△EOF∽△ABO。
(2)在运动过程中,无论 t 取何值,总有$EF ⊥ OA$,为什么?根据题意得OE=1.5tcm，OF=2tcm，∵AB=3cm，OB=4cm，∴$\frac{OE}{AB}$=$\frac{OF}{BO}$=$\frac{t}{2}$，∵∠EOF=∠ABO=90°，∴Rt△EOF∽Rt△ABO，∴∠AOB=∠EFO，∵∠AOB+∠FOC=90°，∴∠EFO+∠FOC=90°，∴∠OCF=90°，∴EF⊥OA，即无论t取何值，总有EF⊥OA。

答案： 解析　
(1)当t=1时，△EOF与△ABO相似，理由如下：
∵t=1，
∴OE=1.5cm，OF=2cm，
∵AB=3cm，OB=4cm，
∴$\frac{OE}{AB}$=$\frac{1.5}{3}$=$\frac{1}{2}$，$\frac{OF}{BO}$=$\frac{2}{4}$=$\frac{1}{2}$，
∴$\frac{OE}{AB}$=$\frac{OF}{OB}$，
∵∠EOF=∠ABO=90°，
∴△EOF∽△ABO。
(2)根据题意得OE=1.5tcm，OF=2tcm，
∵AB=3cm，OB=4cm，
∴$\frac{OE}{AB}$=$\frac{OF}{BO}$=$\frac{t}{2}$，
∵∠EOF=∠ABO=90°，
∴Rt△EOF∽Rt△ABO，
∴∠AOB=∠EFO，
∵∠AOB+∠FOC=90°，
∴∠EFO+∠FOC=90°，
∴∠OCF=90°，
∴EF⊥OA，即无论t取何值，总有EF⊥OA。